2.2.1 Champ gravitationnel terrestre
Gravimétrie
La gravimétrie est une méthode géophysique qui étudie les variations spatiales du champ de gravité. Localement, le champ de gravité mesurable sur la surface terrestre varie en raison de la distribution hétérogène de la densité du sol. Régionalement, elle est affectée par la topographie (montagnes, vallées, etc). Les variations dans la gravité peuvent aussi être temporelles à cause de la force de marée, de la tectonique des plaques ou de la fonte des glaciers, par exemple.
En géophysique appliquée, on s’intéresse surtout aux variations locales de l’accélération gravitationnelle causées par les hétérogénéités de densité dans le sol, c’est-à-dire seulement les variations causées par des changements dans la géologie. Il serait donc utile d’avoir un niveau de référence (une valeur théorique) de la gravité afin de ramener les valeurs mesurées à ce niveau. Se faisant on peut se concentrer uniquement sur les variations observées par rapport à la gravité théorique.
Cette section couvre deux modèles qui permettent de décrire l’accélération gravitationnelle théorique sur Terre. Le premier modèle, celui de l’ellipsoïde, est assez simplifié. Le second modèle est celui du géoïde. Ce dernier est un peu plus précis que l’ellipsoïde, car il tient compte des déformations de la surface terrestre (Figure 1).
Figure 1. Schéma simplifié d’une section de la surface terrestre montrant la différence entre le modèle de l’ellipsoïde et le modèle du géoïde. Les dimensions sont exprimées en unités arbitraires (u.a.).
En fait, le géoïde est défini comme étant une surface perpendiculaire à la gravité en tout point (Figure 2). C’est donc une des surfaces équipotentielles du champ gravitationnel.
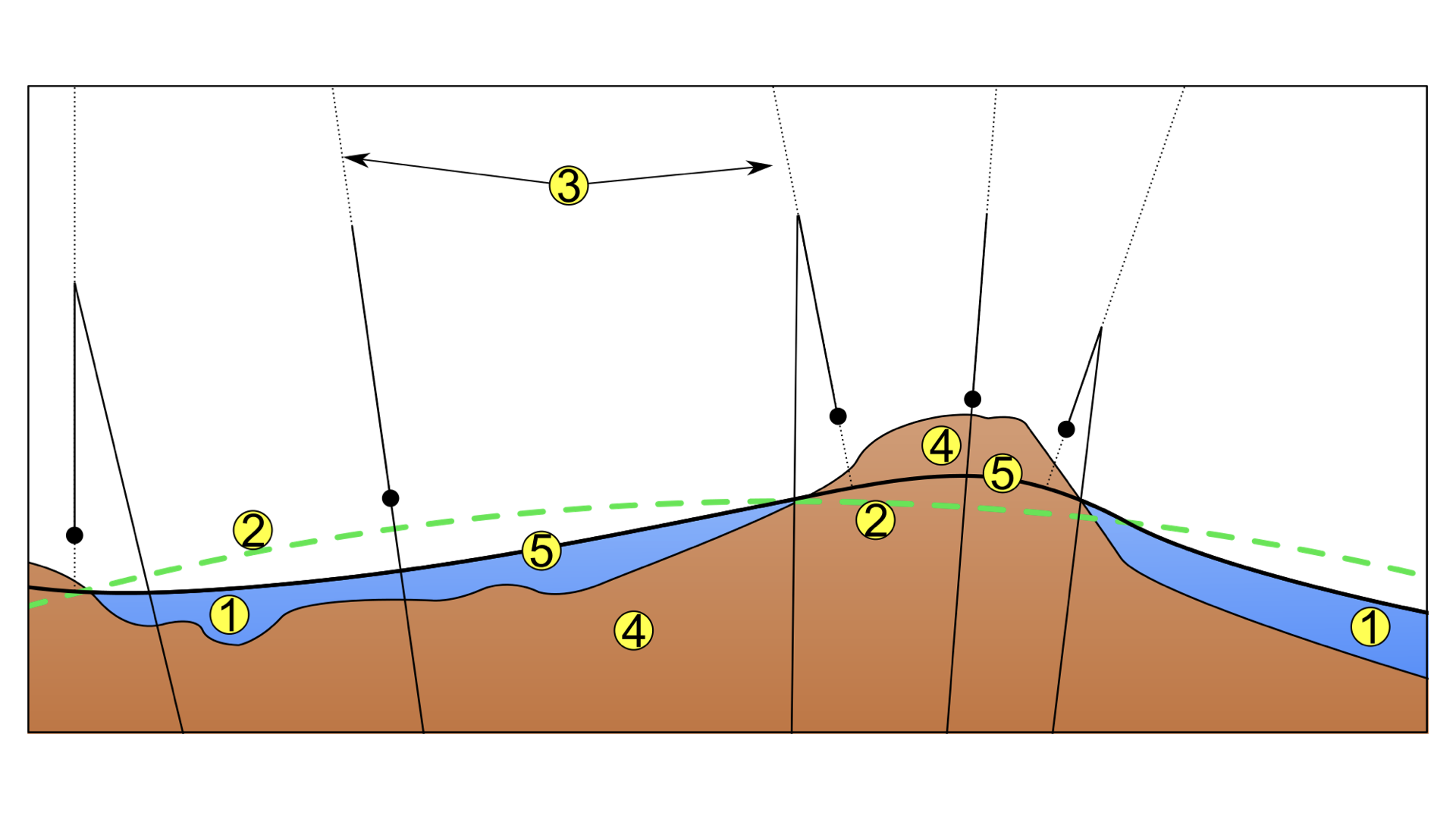
Figure 2. Schéma montrant la différence entre le modèle de l’ellipsoïde et le modèle du géoïde. 1 : Océans. 2 : Ellipsoïde de référence. 3 : Pendule au repos. 4 : Continents et montagnes. 5 : Géoïde de référence. Source.
Ellipsoïde
La forme de la Terre peut être approximée par un ellipsoïde qui tourne sur lui-même. En effet, la Terre est légèrement aplatie aux pôles par rapport à l’équateur, et ce à cause de sa rotation. Si $R_\mathrm{e}$ est le rayon de la Terre à l’équateur et que $R_\mathrm{p}$ est le rayon de la Terre aux pôles (Figure 3), alors l’excentricité $e_\mathrm{T}$ de l’ellipsoïde de la Terre est
\[e_\mathrm{T} = \sqrt{1 - \frac{R_\mathrm{p}^2}{R_\mathrm{e}^2}} \approx 0.081,\]Même si l’excentricité de la Terre est presque nulle, celle-ci ne peut pas être considérée comme une sphère parfaite. Notez que plusieurs livres de références utilisent toutefois le terme “sphéroïde” au lieu d’ellipsoïde.
Figure 3. Schéma montrant l’aplatissement de la Terre aux pôles.
Deux composantes affectent l’accélération gravitationnelle ressentie à la surface de l’ellipsoïde.
Aplatissement aux pôles
Une particule située sur la surface de la Terre à une latitude $\phi$ se trouve à une distance $r$ du centre de la Terre. En effet,
- si $\phi \to 0$, alors $r \to R_\mathrm{e} $ et
- si $\phi \to \pi/2$, alors $r \to R_\mathrm{p} $.
Souvenez-vous que l’accélération gravitationnelle causée par la masse de la Terre varie en $1/r^2$. L’accélération est donc plus forte aux pôles et plus faible à l’équateur.
Accélération centrifuge
Si la Terre tourne autour de son axe avec une vitesse angulaire $\omega$, alors l’accélération centrifuge $a_\mathrm{n}$ (normale à la surface) ressentie à un point quelconque de la Terre situé aux coordonnées $(r, \phi)$ est
\[a_\mathrm{n} = \omega^2 r \cos \phi .\]Remarquez que
- si $\phi \to 0$, alors $a_\mathrm{n} \to \omega^2 R_\mathrm{e}$ et
- si $\phi \to \pi/2$, alors $a_\mathrm{n} \to 0 $.
Conséquemment l’accélération centrifuge normale est nulle aux pôles et maximale à l’équateur. Elle agit dans la direction opposée de l’accélération gravitationnelle à tous points de la surface Terrestre.
Le concept d’accélération centrifuge est illustré à la Vidéo 1, où la longueur du vecteur représentant l’accélération centrifuge augmente avec le carré de la vitesse angulaire du point rouge.
Vidéo 1. Simulation de l’accélération centrifuge ressentie sur un point en rotation.
Il faut comprendre que l’accélération centrifuge est en fait causée par une force fictive qui se manifeste en réaction à la force centripète (voir la troisième loi de Newton). La force centripète est celle qui maintient un objet dans un mouvement circulaire.
Gravité théorique
Dans le système géodésique WGS84, la gravité théorique ($g_\mathrm{th}$) à la surface de la Terre est donnée par
\[g_\mathrm{th}(\phi )=9.7803253359\left[{\frac {1+0.00193185265241\sin ^{2}(\phi )}{\sqrt {1-0.00669437999013\sin ^{2}(\phi )}}}\right] ,\]où $g_\mathrm{th}$ est exprimée en unités SI (m/s$^2$). La composante d’accélération axifuge est responsable d’environ les deux tiers de la différence de gravité entre l’équateur et les pôles. Le tiers restant est attribuable à l’aplatissement.
Nous verrons plus tard que la dépendance de la gravité avec la latitude n’est pas négligeable lors d’un levé gravimétrique. En effet il faut toujours corriger les données pour tenir compte des changements de latitude sur l’ellipsoïde de référence.
Géoïde
Le géoïde est la surface équipotentielle perpendiculaire à la direction de l’attraction gravitationnelle en tout point de la surface terrestre (Figure 1). Effectivement, la direction de la gravité n’est pas partout perpendiculaire à la surface de l’ellipsoïde. Pourquoi? Parce qu’il existe d’importantes hétérogénéités horizontales sur et sous la surface terrestre. Ces hétérogénéités incluent les différences d’élévation entre la croûte continentale et la croûte océanique et les variations de densité dans le manteau.
L’élévation du géoïde peut être mesuré à l’aide de stations gravimétriques partout dans le monde. Vous pouvez visualiser l’élévation du géoïde avec les modèles 3D interactifs suivants, où la composante verticale a été fortement exagérée.
Liens intéressants
- Vous avez une imprimante 3D? Imprimez votre propre géoïde à partir des données de NOAA (la bibliothèque de Polytechnique Montréal offre aussi un service d’impression 3D).