4.3.1 Relation de Poisson
Similarités entre le magnétisme et la gravité
Potentiel gravitationnel
Vous devriez avoir maintenant compris que le champ gravitationnel et le potentiel magnétique sont très similaires. Reprenons la loi universelle de l’attraction gravitationnelle sous forme vectorielle :
\[\boldsymbol{g}(P) = -G \frac{m}{r^2}\ \boldsymbol{\hat{r}} ,\]où $G$ est la constante gravitationnelle, $m$ est la masse qui génère le champ, $r$ est la distance entre cette masse et le point d’observation $P$ et $\boldsymbol{\hat{r}}$ pointe de $m$ vers $P$. On a aussi vu que le potentiel gravitationnel ($U$, section 2.3.1) pour une distribution de masse uniforme dans un volume $v$ est
\[U(P) = -G \rho \int_v \frac{1}{r}\ dv ,\]où $\rho$ est la densité volumique de masse de la distribution. Enfin, on sait que $\boldsymbol{g}= -\nabla U$ parce que $\boldsymbol{g}$ est un champ conservatif.
Potentiel magnétique
Le potentiel scalaire magnétique (section 4.1.4), de façon générale, s’écrivait comme
\[V(P) = -C_m \boldsymbol{m} \cdot \nabla_P \frac{1}{r} ,\]où $C_m=\mu_0/4\pi$, $\boldsymbol{m}$ est le moment magnétique, $\nabla_P (1/r) = -\boldsymbol{\hat{r}}/r^2$ et $r$ est la distance entre la source du champ et un point d’observation $P$. On voit donc immédiatement que pour un point d’observation donné, le champ gravitationnel $\boldsymbol{g}$ et le potentiel magnétique $V$ créé par un dipôle ont tous les deux une dépendance en $1/r^2$ et sont proportionnels à l’intensité de leurs sources respectives.
Souvenez-vous aussi que l’aimantation ($\boldsymbol{M}$) est définie comme $\boldsymbol{M} = \sum_i \boldsymbol{m}_i$ (Chapitre 1). Donc le potentiel d’une distribution uniforme de moments magnétiques est
\[V(P) = -C_m \boldsymbol{M} \cdot \nabla_P \int_v \frac{1}{r}\ dv ,\]Les potentiels sont reliés?
Pour un corps de densité uniforme $\rho$ et d’aimantation uniforme $\boldsymbol{M}$, les potentiels gravitationnel et magnétique contiennent tout deux la même intégrale. En effet, on peut mettre l’équation (2) dans l’équation (4) et on obtient
\[V(P) = \frac{C_m}{G\rho}\boldsymbol{M}\cdot\nabla U ,\]où $-\nabla U = \boldsymbol{g}$ parce que c’est un champ conservatif. Ça veut dire que le potentiel magnétique d’un corps dont la densité et l’aimantation sont uniformes peut être obtenu par son attraction gravitationnelle! En écrivant de façon explicite le produit scalaire de l’équation (5) on obtient finalement :
\[V(P) = -\frac{C_m}{G\rho}Mg\cos{\theta} ,\]où $\theta$ est l’angle entre l’aimantation du corps et la direction du champ gravitationnel. C’est la relation de Poisson.
La relation de Poisson
La relation de Poisson (équation 6) dit que le potentiel magnétique est proportionnel à la composante du champ gravitationnel qui va dans la même direction que l’aimantation. Cette relation est valide si et seulement si :
- Le corps aimanté est le même que celui qui crée le champ de gravité (même géométrie),
- L’aimantation et la densité du corps sont uniformes.
Visuellement, on peut voir la relation de Poisson à la Figure 1.
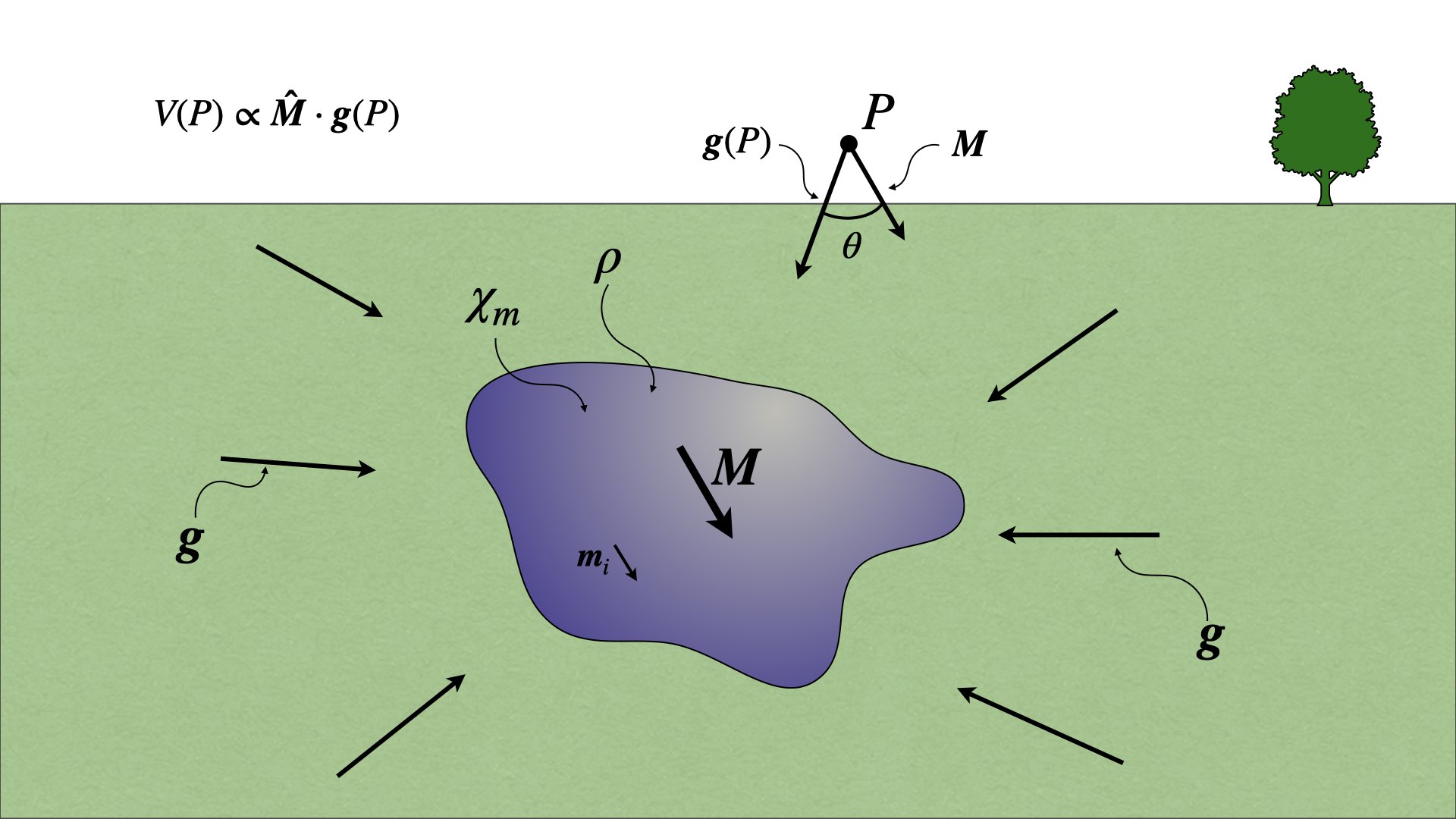
Figure 1. Représentation vectorielle de la relation de Poisson.
Extension par principe de superposition
Dans la réalité, on pourrait croire que la condition qui veut que la densité et l’aimantation du corps soit uniforme est rarement respectée. Pensez-y, ça demanderait à ce que la composition minéralogique de la roche soit plus ou moins uniforme. Suite à vos cours de pétrographie et de minéralogie vous avez sans doute remarqué que la plupart des roches sont loin d’être uniformes. Cependant, si on décompose un échantillon de roche en ses divers constituants minéralogiques, on peut facilement faire l’approximation que chaque constituant a des propriétés pétrophysiques uniformes.
Par exemple, les grains de quartz dans la roche auront tous une densité et une susceptibilité magnétique semblable d’un à l’autre. Les grains de magnétite auront une densité et une susceptibilité beaucoup plus élevée que le quartz, mais d’un grain de magnétite à l’autre, des propriétés physiques semblables seront observées. Il en découle que la relation de Poisson serait respectée pour chaque constituant de la roche. Plus macroscopiquement parlant, on pourrait argumenter que la relation est respectée pour chaque unité lithologique parmi un ensemble d’unités formant un groupe lithologique. Selon le principe de superposition, si la relation de Poisson est respectée pour chaque constituant alors elle est respectée pour l’ensemble des constituants. La relation de Poisson devrait donc être valide pour tous les contextes géologiques où :
- L’aimantation des constituants est proportionnelle à leur densité,
- L’aimantation est uniforme (direction et amplitude constante du champ primaire).
Il reste toutefois une certaine ambiguïté. Par exemple, la pyrrhotite et la pyrite sont des minéraux qui ont une densité semblable. Cependant, la pyrite est un minéral diamagnétique (susceptibilité magnétique près de 0), alors que la pyrrhotite, sous certaines formes crystallines, est paramagnétique (susceptibilité magnétique positive). Il s’agit ici d’un contre-exemple assez évident où la relation de Poisson de tient pas la route. Si ce genre de contre-exemple n’existait pas, on pourrait argumenter que la méthode magnétique est inutile, puisqu’on pourrait calculer le champ magnétique partout où on a réalisé des levés de gravimétrie! Mais soyez rassurés, la méthode magnétique et la relation de Poisson sont très utiles en géophysique appliquée.
Applications de la relation de Poisson
Pseudogravité
La première application évidente de la relation de Poisson est la transformation des anomalies de champ total en anomalies de pseudogravité. Ça peut être utile parce que les mesures magnétiques prennent moins de temps à se réaliser que les mesures de gravité. On peut donc couvrir de plus grandes distances avec des meilleures résolutions avec la méthode magnétique. En faisant la transformation du potentiel magnétique vers la valeur de pseudogravité, on peut estimer la réponse gravimétrique de la région et ce de façon plus ou moins gratuite!
Modélisation magnétique
La deuxième application évidente est le calcul des réponses magnétiques attendues à partir des modèles de gravité qu’on a déjà défini dans la section 2.4. En effet, il est souvent plus facile de calculer analytiquement la réponse de gravité des géométries simples, comme les sphères, les cylindres et les prismes, que de calculer leurs réponses magnétiques. C’est parce que l’attraction gravitationnelle est toujours radiale alors que le champ d’aimantation (champ secondaire) s’apparente à celui d’un dipôle.
Exemples
Une sphère
On sait que la gravité causée par une sphère est
\[\boldsymbol{g} = -G\rho\left(\frac{4\pi a^3}{3}\right) \frac{1}{r^2}\ \boldsymbol{\hat{r}} ,\]où $a$ est le rayon de la sphère. La relation de Poisson permet de trouver le potentiel magnétique de la sphère :
\[V = C_m \left(\frac{4\pi a^3}{3}\right) \frac{M}{r^2} \boldsymbol{\hat{M}}\cdot\boldsymbol{\hat{r}} .\]D’après la définition de l’aimantation, on a que $\boldsymbol{m} = v\boldsymbol{M}$, où $v$ est le volume de la sphère. On retrouve finalement l’équation d’un dipôle :
\[V = C_m \frac{\boldsymbol{m}\cdot\boldsymbol{\hat{r}}}{r^2} ,\]ce qui nous dit que le potentiel magnétique d’une sphère est le même que celui d’un dipôle magnétique qui serait placé à son centre. Encore un parallèle avec la gravité! On trouve ensuite les trois composantes de $\boldsymbol{B}$ avec la relation $\boldsymbol{B} = -\nabla V$ en coordonnées sphériques.
Une tranche de Bouguer
La gravité de d’une tranche de Bouguer est
\[\boldsymbol{g} = -2\pi G\rho t\ \boldsymbol{\hat{n}} ,\]ou $t$ est l’épaisseur de la tranche et $\boldsymbol{\hat{n}}$ est le vecteur normal à la tranche. Si la tranche de Bouguer est uniformément aimantée selon la même direction que la gravité, pour un point donné sur tranche, alors
\[V = -2\pi C_m M t .\]Ce résultat indique que le potentiel magnétique d’une tranche de Bouguer est constant. D’après la relation $\boldsymbol{B} = -\nabla V$ ça veut dire que le champ magnétique d’une tranche de Bouguer uniformément aimantée est nul.
Un cylindre horizontal infini
Le champ gravitationnel d’un cylindre horizontal infini est donné par (section 2.4.1) :
\[\boldsymbol{g} = -2\pi G R^2 \rho\frac{1}{r}\ \boldsymbol{\hat{r}},\]où $R$ est le rayon du cylindre. D’après la relation de Poisson le potentiel magnétique du cylindre est
\[V = -2\pi R^2 C_m \frac{\boldsymbol{m}\cdot\boldsymbol{\hat{r}}}{r} ,\]ce qui correspond au potentiel d’une série de dipôles alignés sur l’axe du cylindre sur toute sa longueur. On trouve ensuite les trois composantes de $\boldsymbol{B}$, comme d’habitude, avec la relation $\boldsymbol{B} = -\nabla V$ en coordonnées cylindriques.