4.1.3 Loi de Gauss en magnétisme
Énoncé
On sait d’après les lois de Maxwell que
\[\nabla \cdot \boldsymbol{B} = 0 ,\]c’est la loi de Gauss en magnétisme. Concrètement, ça veut dire qu’on ne peut pas isoler une source nette du champ $\boldsymbol{B}$ dans un volume de l’espace. En d’autres mots, il n’existe pas de monopôles magnétiques dans la nature, contrairement aux masses et aux charges électriques. Ceci est valide partout : dans le vide et dans la matière.
Forme intégrale
Si on intègre l’équation (1) sur un volume quelconque $V$, on obtient
\[\iiint_V \nabla \cdot \boldsymbol{B}\,\mathrm{d}V = 0 .\]Et en applicant le théorème de la divergence l’équation est aussi équivalente à :
\[\begin{align} \iiint_V \nabla \cdot \boldsymbol{B}\,\mathrm{d}V & = \iint_S \boldsymbol{B}\cdot\mathrm{d}\boldsymbol{S}\\ &= 0 ,\end{align}\]où $\mathrm{d}\boldsymbol{S} = \boldsymbol{\hat{n}}\,\mathrm{d}S$ est un vecteur partout normal à la surface $S$.
Ca veut dire que la composante de $\boldsymbol{B}$ qui est normale à une surface fermée quelconque est nulle si on l’intègre sur toute cette surface. En d’autres mots, le flux total de $\boldsymbol{B}$ au travers de $S$ est nul (Figure 1).
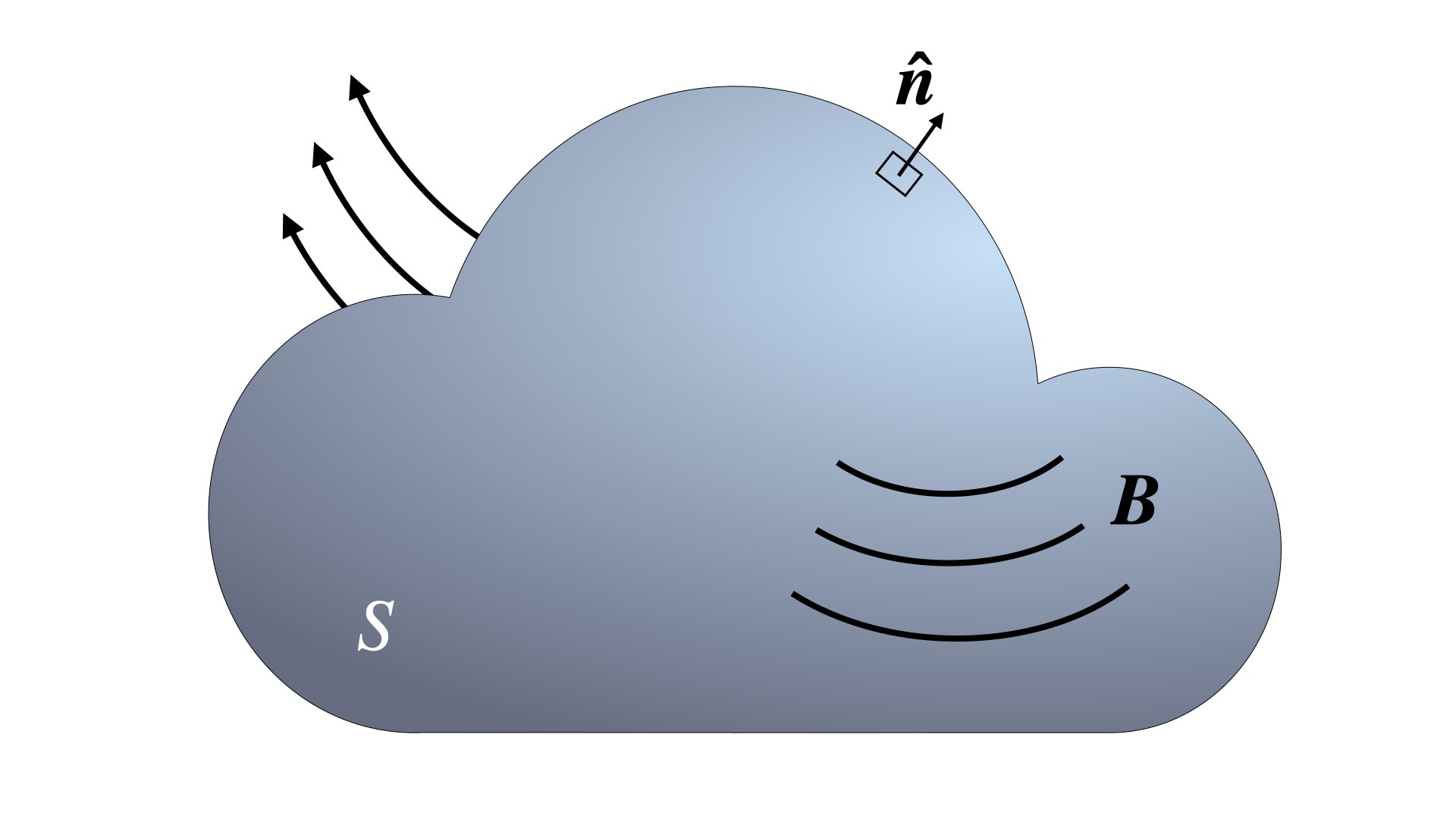
Figure 1. Schéma montrant un champ $\boldsymbol{B}$ qui traverse une surface $S$. Le vecteur $\boldsymbol{\hat{n}}$ est partout perpendiculaire à $S$ et pointe vers l’extérieur.
Implications en magnétométrie
Supposons qu’on mesure le champ magnétique partout sur une surface (un levé magnétique à la surface terrestre, par exemple). Cette surface n’est pas fermée. Pour obtenir une surface fermée on va utiliser la surface plane d’un hémisphère sphérique (Figure 2). On suppose que toutes les sources magnétiques sont sous l’hémisphère (tous les géomatériaux magnétiques sont sous la surface du sol). La surface plane de l’hémisphère est dénotée $S_1$ et la surface courbe est dénotée $S_2$.
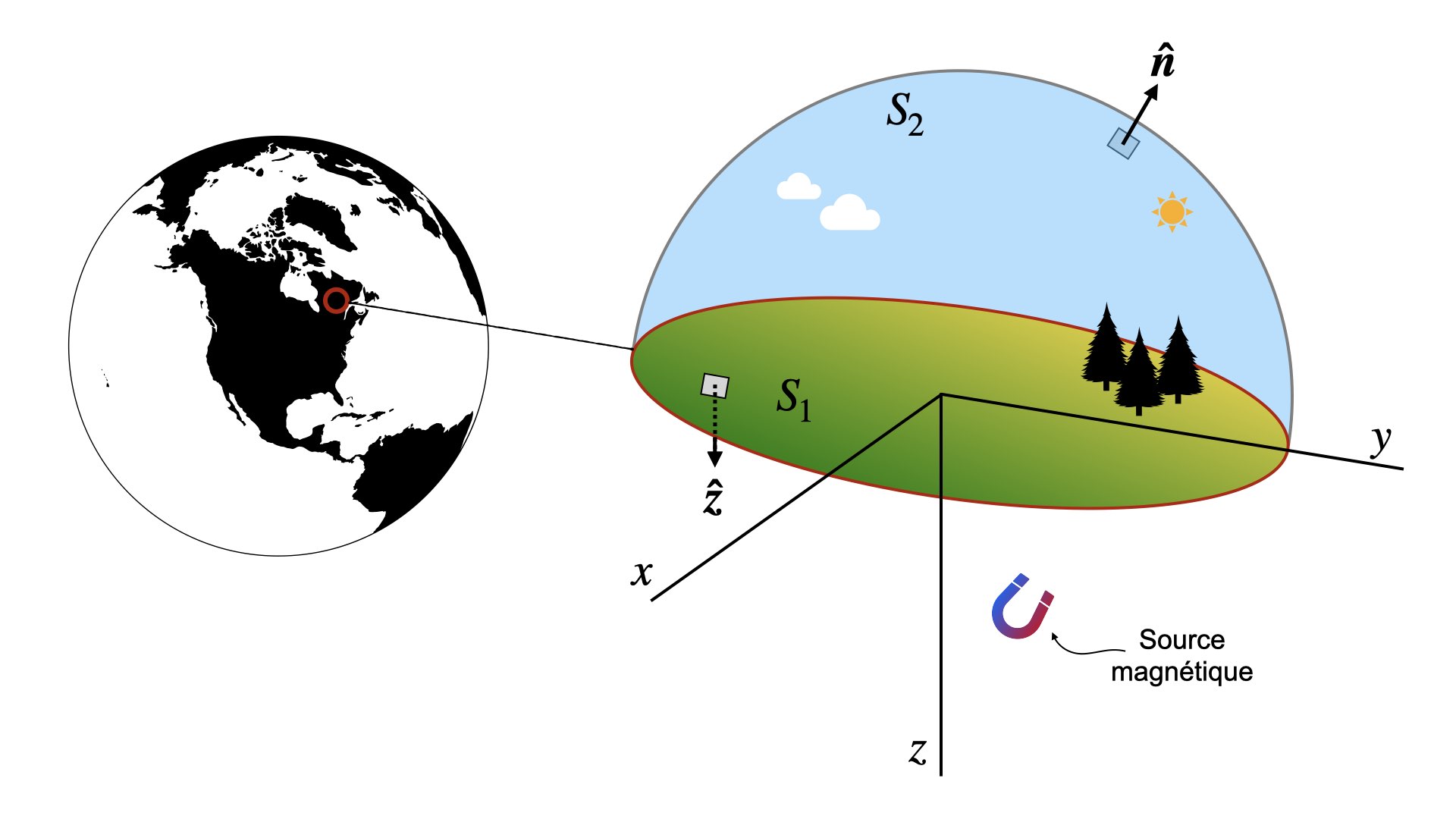
Figure 2. Schéma montrant une source magnétique située sous la surface du sol et qui génère un champ $\boldsymbol{B}$. Le flux total qui traverse la surface formée par $S_1$ et $S_2$ est nul.
La loi de Gauss en magnétisme dit que
\[\iint_S \boldsymbol{B}\cdot\mathrm{d}\boldsymbol{S} = 0 ,\]donc que
\[\iint_{S_1} \boldsymbol{B}\cdot\boldsymbol{\hat{z}}\,\mathrm{d}S_1 + \iint_{S_2} \boldsymbol{B}\cdot\boldsymbol{\hat{n}}\,\mathrm{d}S_2 = 0 .\]Si la surface du levé est beaucoup plus grande que les dimensions des sources magnétiques, la surface $S_2$ s’éloigne des sources et on peut montrer que son intégrale est nulle. Ça veut dire que
\[\iint_{S_1} \boldsymbol{B}\cdot\boldsymbol{\hat{z}}\,\mathrm{d}S_1 = 0 ,\]donc que le flux net de $\boldsymbol{B}$ sur toute la surface du levé magnétique est nul. Ça implique que sur un levé donné, il devrait y avoir autant d’anomalies positives que négatives. Si ce n’est pas le cas, c’est qu’il existe des effets régionaux (dont les sources ont des dimensions comparables aux dimensions du levé).