4.2.4 Anomalies crustales
Profondeur des sources magnétiques
Les deux sources internes qui contribuent au champ géomagnétique se situent à des niveaux différents dans la Terre. Comme on l’a déjà dit, c’est principalement des processus dans le noyau externe qui sont responsables du champ, mais il y aussi une bonne composante qui provient de la croûte terrestre.
Figure 1. Schéma simplifié de la structure interne de la Terre. Image du domaine public.
Coûte terrestre
Dans la croûte terrestre, la température de la plupart des roches sont à une température inférieure à la température de Curie des minéraux ferro/ferrimagnétiques qu’elles contiennent. Ça veut dire que les roches dans la croûte peuvent conserver une aimantation permanente. À grande échelle, les régions de la croûte qui sont riches en oxydes de fer (p. ex. magnétite) agissent comme des sources du champ magnétique qui est mesurable à la surface. Il existe des endroits où l’isotherme de la température de Curie de la magnétite est à un niveau plus élevé que la limite entre le manteau et la croûte. À ses endroits, sous l’isotherme, la roche est paramagnétique (pas d’aimantation permanente).
Manteau
Bien qu’il existe des sources de magnétisme dans le manteau, plus particulièrement sous les océans, celles-ci ne contribuent pas beaucoup au champ magnétique mesuré à la surface. De plus, le manteau étant situé sous l’isotherme de la température de Curie de la magnétite, cette région de la Terre est considérée non magnétique.
Noyau externe
C’est la source du champ magnétique primaire.
Séparation des sources magnétiques
Les sources des anomalies recherchées en géophysique appliquée se situent dans la croûte terrestre. Comme il y a une énorme différence de profondeur entre la croûte et le noyau externe, qui sont les deux sources interne du champ géomagnétique, on va démontrer dans cette section qu’il est possible d’isoler la composante crustale avec la décomposition en harmoniques sphériques.
Spectre de puissance
On se souvient que le potentiel scalaire ($V$) du champ géomagnétique ($\boldsymbol{B}$) est
\[V = a\sum_{n=1}^{\infty} \left(\frac{a}{r}\right)^{n+1} \sum_{m=0}^n (g_n^{m}\cos{m\phi} + h_n^{m}\sin{m\phi})\ P_n^m(\theta) ,\]où $a$ est le rayon de la Terre, $g$ et $h$ sont les coefficients de Gauss donnés par l’IGRF et $P_n^m$ est le polynome associé de Legendre de degré $n$ et d’ordre $m$. De plus,
\[\boldsymbol{B} = -\nabla V .\]Chaque terme dans la décomposition (chaque degré $n$) est caractérisé par une importance relative parmi la somme totale de toutes les contributions. Il est possible de quantifier l’importance de chacun des degrés d’approximation en calculant le spectre de puissance de la série.
⚠️ Voyez-vous la ressemblance avec la transformation de Fourier et son spectre de puissance?
Le spectre de puissance est donné par
\[R_n = \frac{1}{4\pi a^2} \int_0^{2\pi}\int_0^{\pi} (\boldsymbol{B}_n \cdot \boldsymbol{B}_n)\ a^2 \sin\theta\ d\theta\phi ,\]où
\[\boldsymbol{B}_n = -\nabla \left[ a\left(\frac{a}{r}\right)^{n+1} \sum_{m=0}^n (g_n^{m}\cos{m\phi} + h_n^{m}\sin{m\phi})\ P_n^m(\theta) \right] .\]La solution de cette équation est donnée par une formule relativement simple [1] :
\[R_n = (n + 1) \sum_{m=0}^n \left[(g_n^m)^2 + (h_n^m)^2\right] .\]Le spectre de puissance ainsi obtenu est tracé à la Figure 2 en fonction du degré $n$ des harmoniques sphériques.
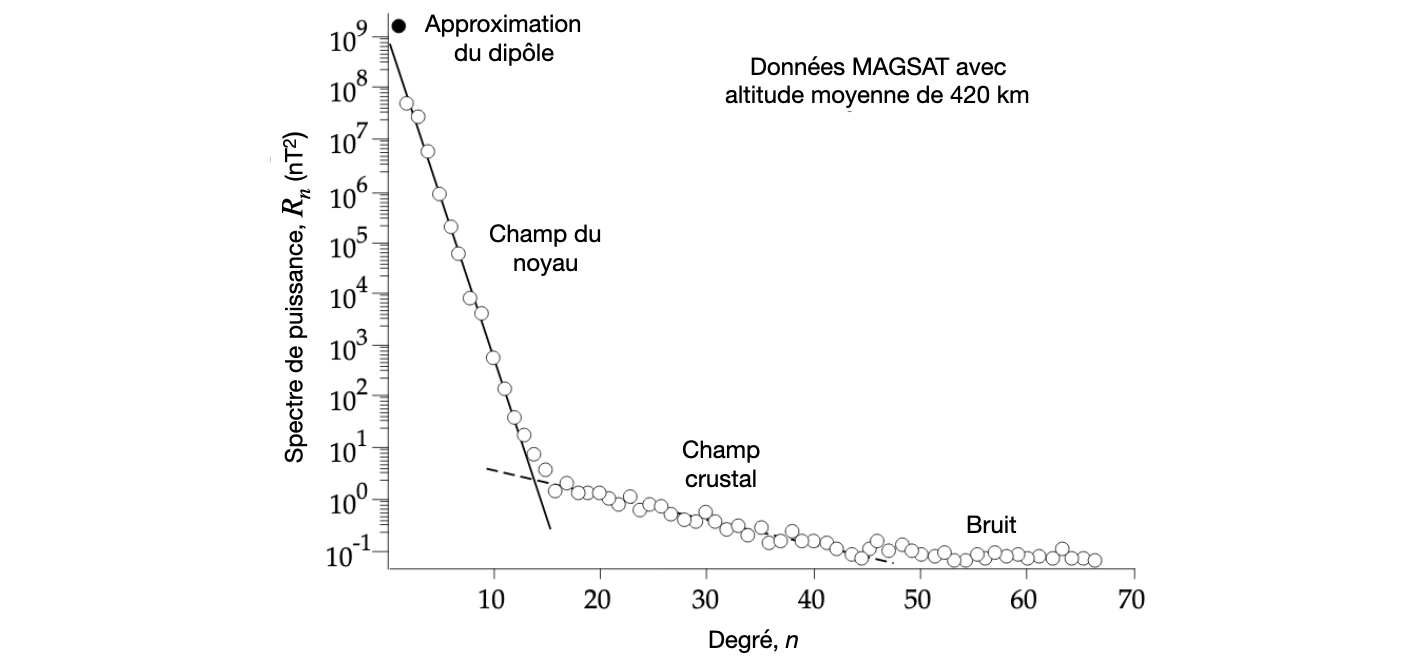
Figure 2. Spectre de puissance de la décomposition du champ magnétique en harmoniques sphériques. Figure modifiée de [2].
Remarquez le point d’inflexion évident à environ $n=15$ sur la Figure 2. Cette coupure dans le spectre de puissance indique la transition entre les composantes du champ géomagnétique générée par le noyau liquide et les composantes générées par la croûte terrestre. Les composantes de degrés supérieurs à $n=45$ ne sont que du bruit ; à partir de ce point l’approximation du champ géomagnétique est optimale.
Justification de la méthode magnétique
Le concept montré à la Figure 2 est fondammental pour justifier l’application de la méthode magnétique en géophysique. Ça implique que lorsqu’on mesure le champ magnétique à la surface terrestre, on devrait être capable d’obtenir seulement la contribution des contrastes de densité dans la croûte terrestre (p. ex. les failles, les anomalies géologiques, les contacts lithologiques, les formations de fer, les variations dans l’épaisseur de la croûte, etc.) en soustrayant la contribution du noyau au champ total mesuré. Toujours d’après la Figure 2, la contribution du noyau peut être obtenue en sommant seulement les termes de degrés 1 à 13.
Pour résumer, il est possible d’isoler les sources dans la croûte terrestre avec les trois étapes suivantes :
- mesurer l’amplitude du champ total (que l’on va dénoter $T$),
- calculer le champ du noyau avec les degrés 1 à 13 de l’IGRF, selon la date du levé,
- soustraire le champ du noyau du champ total.
Cette approximation est valable pour les levés magnétiques aux échelles locales et régionales qu’on réalise pour des applications géologiques. Pour conclure, il est justifié d’utiliser la méthode magnétique pour cartographier la géologie.
Références
- Blakely, R. J. (1995). « The Geomagnetic Field », dans Potential Theory in Gravity and Magnetic Applications, Cambridge: Cambridge University Press, p. 154–181.
- Lowrie, W. (2007). « Geomagnetism and paleomagnetism », dans Fundamentals of Geophysics, Cambridge: Cambridge University Press, p. 281–362.