4.1.4 Potentiel magnétique
Théorème d’Helmholtz
On sait que si un champ $\boldsymbol{F}$ est conservatif, alors on peut le représenter comme le gradient d’un potentiel scalaire $\phi$ :
\[\boldsymbol{F} = \nabla\phi .\]En fait, dans sa forme générale le théorème d’Helmholtz dit qu’on peut représenter un champ conservatif comme le gradient d’un potentiel scalaire plus le rotationnel d’un potentiel vecteur $\boldsymbol{A}$, tel que
\[\boldsymbol{F} = \nabla\phi + \nabla\times\boldsymbol{A} .\]Les deux formes du potentiel sont une façon différente d’exprimer $\boldsymbol{F}$. Pour le champ gravitationnel ($\boldsymbol{g}$), le deuxième terme était nul parce que $\boldsymbol{g}$ est irrotationnel. Pour le champ magnétique ($\boldsymbol{B}$), il existe toujours un potentiel vecteur, et le potentiel scalaire du champ magnétique existe seulement dans certaines conditions.
Potentiel magnétique scalaire
Il est particulièrement intéressant de définir quand le potentiel scalaire du champ magnétique existe, parce que ça voudrait dire qu’on peut traiter les données magnétiques de la même façon que les données gravimétriques. La loi d’Ampère (2e équation de Maxwell) dit que pour un milieu,
\[\nabla\times\boldsymbol{B} = \mu_0 \boldsymbol{J}_t ,\]où $\boldsymbol{J}_t$ représente la somme des densités de courants qui passent dans le milieu (somme des courants macroscopiques, de polarisation et de magnétisation).
Le flux de cette densité de courant au travers d’une surface $S$ quelconque (Figure 1) est obtenu en intégrant l’équation (3) sur cette surface :
\[\iint_S \nabla\times\boldsymbol{B}\cdot\mathrm{d}\boldsymbol{S} = \mu_0 \iint_S \boldsymbol{J}_t\cdot\mathrm{d}\boldsymbol{S} ,\]où $\mathrm{d}\boldsymbol{S} = \boldsymbol{\hat{n}}\,\mathrm{d}S$.
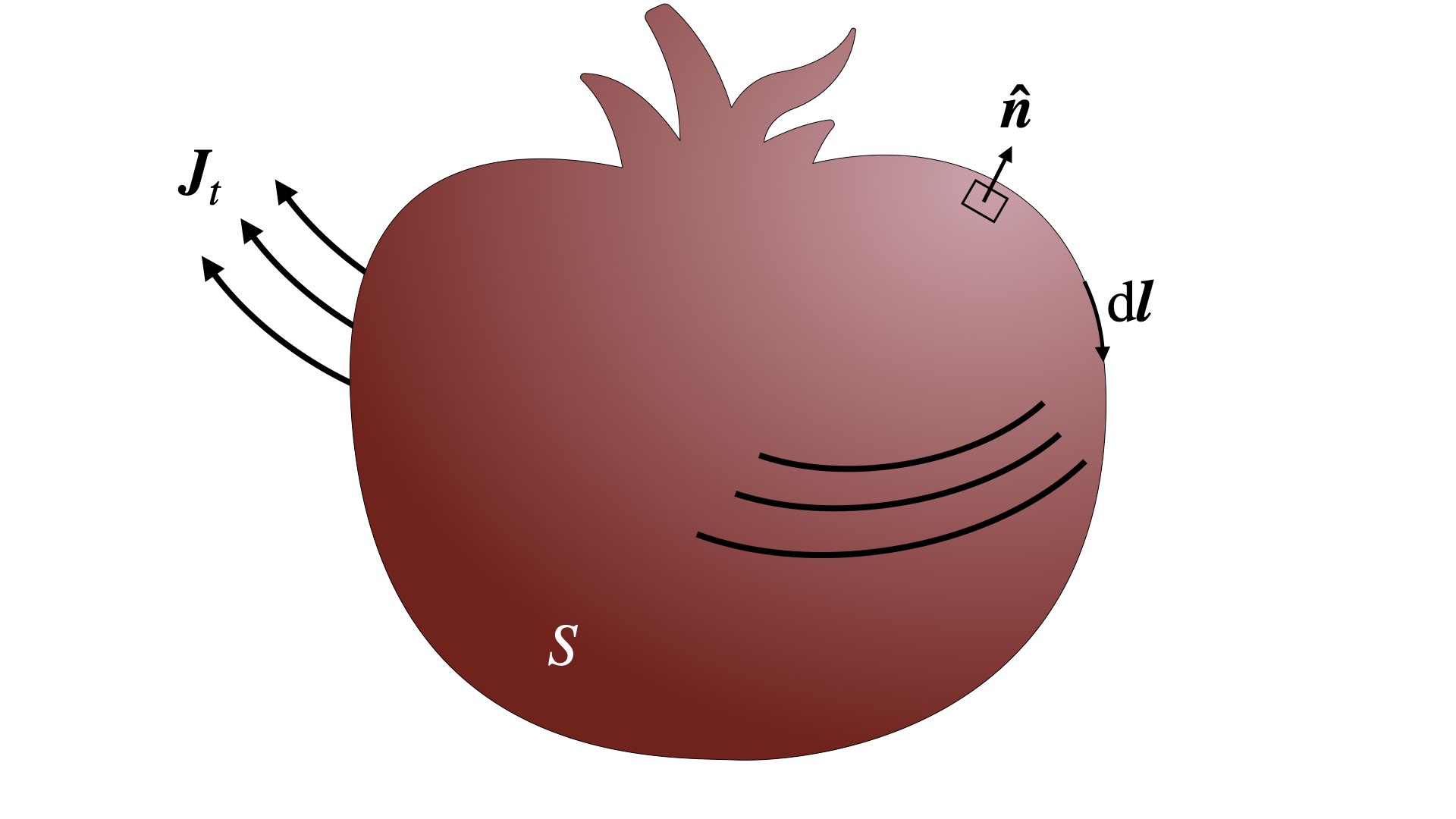
Figure 1. Schéma montrant la somme des densités de courant ($\boldsymbol{J}_t$) qui traversent une surface $S$. Le vecteur $\boldsymbol{\hat{n}}$ est partout perpendiculaire à $S$ et pointe vers l’extérieur. L’élément de chemin $\mathrm{d}\boldsymbol{l}$ fait une boucle autour de la périphérie de $S$.
Si on applique le théorème de Stokes l’équation (4) devient
\[\oint \boldsymbol{B}\cdot\mathrm{d}\boldsymbol{l} = \mu_0 \iint_S\boldsymbol{J}_t\cdot\mathrm{d}\boldsymbol{S} .\]Si la somme des densités de courants est nulle ($\boldsymbol{J}_t = 0$), alors on remarque que
\[\oint \boldsymbol{B}\cdot\mathrm{d}\boldsymbol{l} = 0 ,\]ce qui implique que le champ $\boldsymbol{B}$ est conservatif et que c’est un champ de potentiel.
Pour différencier le potentiel gravitationnel ($U$) du potentiel magnétique, on va utiliser $V$ pour dénoter ce dernier :
\[\boldsymbol{B} = -\nabla V .\]En résumé, $\boldsymbol{B}$ peut être exprimé comme un potentiel scalaire $V$ si et seulement si il n’y a pas de déplacement de charges (courants) dans le milieu où on mesure le champ magnétique. En géophysique, on fait souvent les mesures à la surface du sol ou du haut des airs, donc à l’extérieur de tout milieu magnétique. Ainsi, cette condition est presque toujours respectée en pratique.
Potentiel d’un dipôle magnétique
Dérivation
On sait d’après la loi de Gauss en magnétisme que les monopôles magnétiques n’existent pas dans la nature. Cependant le concept de monopôle peut être utilisé avec le principe de superposition pour dériver l’équation d’un dipôle magnétique.
Soit une «charge» magnétique de signe $+q_m$ située à l’origine et une «charge» de signe opposé $-q_m$ située à une distance $\Delta z$ sous la première (Figure 2).
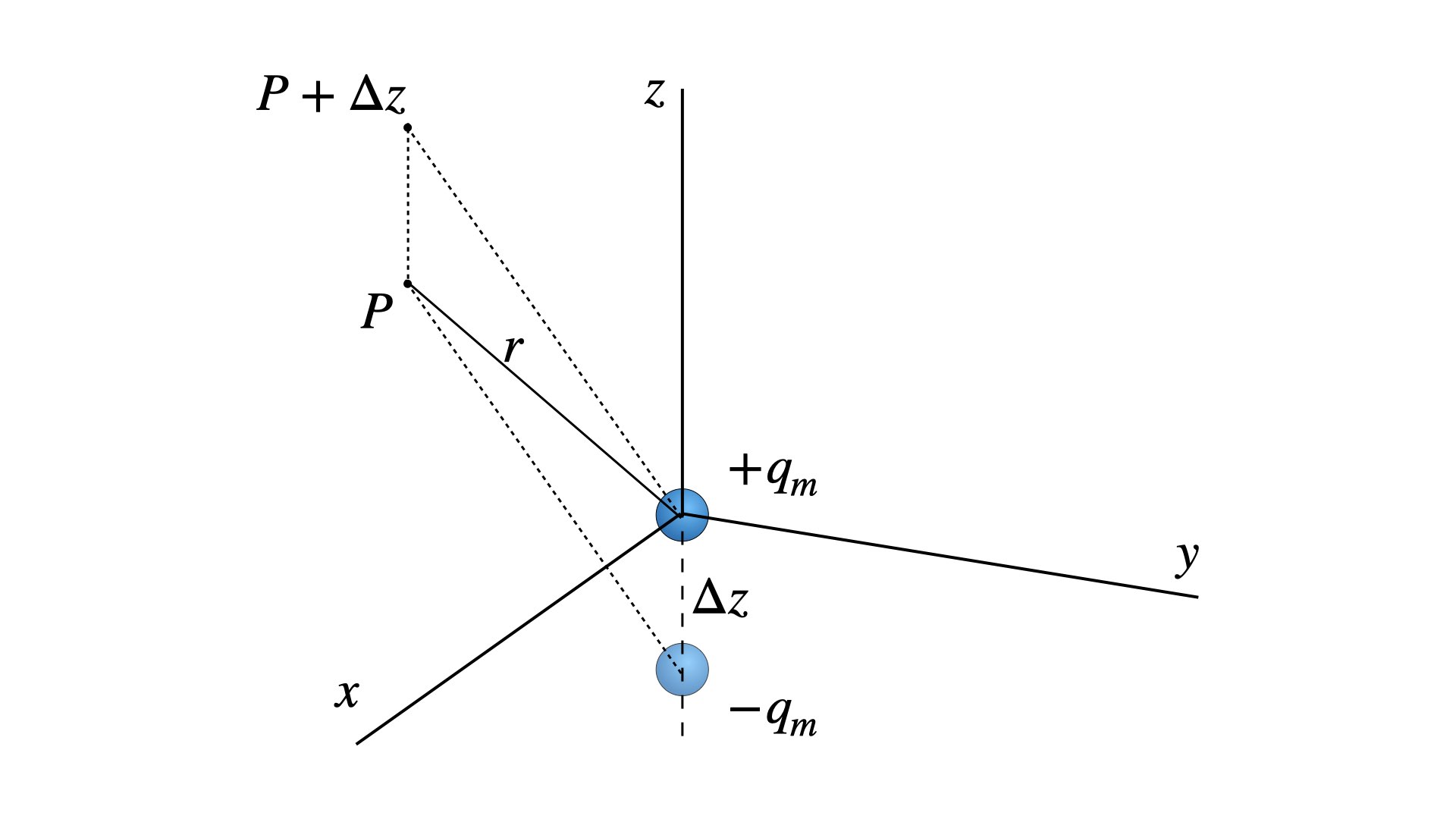
Figure 2. Schéma d’un dipôle magnétique.
D’après le principe de superposition, le potentiel au point $P$ est la somme du potentiel causé par la charge $+q_m$ ($V_1$) et du potentiel causé par la charge $-q_m$ ($V_2$):
\[\begin{equation*} V(P) = V_1(P) + V_2(P). \end{equation*}\]Avec la méthode des images on peut dire que le potentiel à $P$ causé par la «charge» négative est égal à $-V_1$ évalué à $P(z+\Delta z$), donc
\[\begin{align*} V(P) &= V_1(P) - V_1(P+\Delta z)\\ & = -[V_1(P+\Delta z) - V_1(P)]. \end{align*}\]On remarque que c’est semblable à la définition d’une dérivée :
\[\frac{\mathrm{d}f}{\mathrm{d}z} = \lim_{\Delta z\to 0}\frac{f(z+\Delta z) - f(z)}{\Delta z} ,\]alors on réécrit le potentiel comme
\[V(P) = -\Delta z \frac{\mathrm{d}V_1(P)}{\mathrm{d}z} .\]Cette relation est valide quand $\Delta z$ est très petit. Par analogie avec le potentiel gravitationnel d’une masse et le potentiel électrique d’une charge électrique,
\[V_1(P) = C_m \frac{q_m}{r} ,\]où $C_m = \mu_0/4\pi$. Alors,
\[V(P) = -C_m q_m \Delta z \frac{\mathrm{d}}{\mathrm{d}z}\frac{1}{r} .\]Il est utile de définir le moment dipolaire magnétique ($\boldsymbol{m}$), tel que
\[\boldsymbol{m} = q_m \boldsymbol{ds} ,\]où $\boldsymbol{ds}$ est le vecteur qui pointe de $+q_m$ à $-q_m$. Ça permet d’écrire le potentiel d’un dipôle de façon plus générale, parce qu’il n’est pas toujours aligné avec $\boldsymbol{\hat{z}}$. Finalement, le potentiel est
\[V(P) = -C_m \boldsymbol{m} \cdot \nabla \frac{1}{r} ,\]où $\nabla$ est l’opérateur différentiel vectoriel.
Potentiel d’une petite boucle
L’équation (13) donne aussi le potentiel causé par le moment dipolaire ($\boldsymbol{m} = AI\ \boldsymbol{\hat{n}}$) d’une boucle d’aire $A$ dans laquelle circule un courant $I$ (Figure 3). Dans ce modèle équivalent, $\boldsymbol{\hat{n}}$ est perpendiculaire à la surface de la boucle.
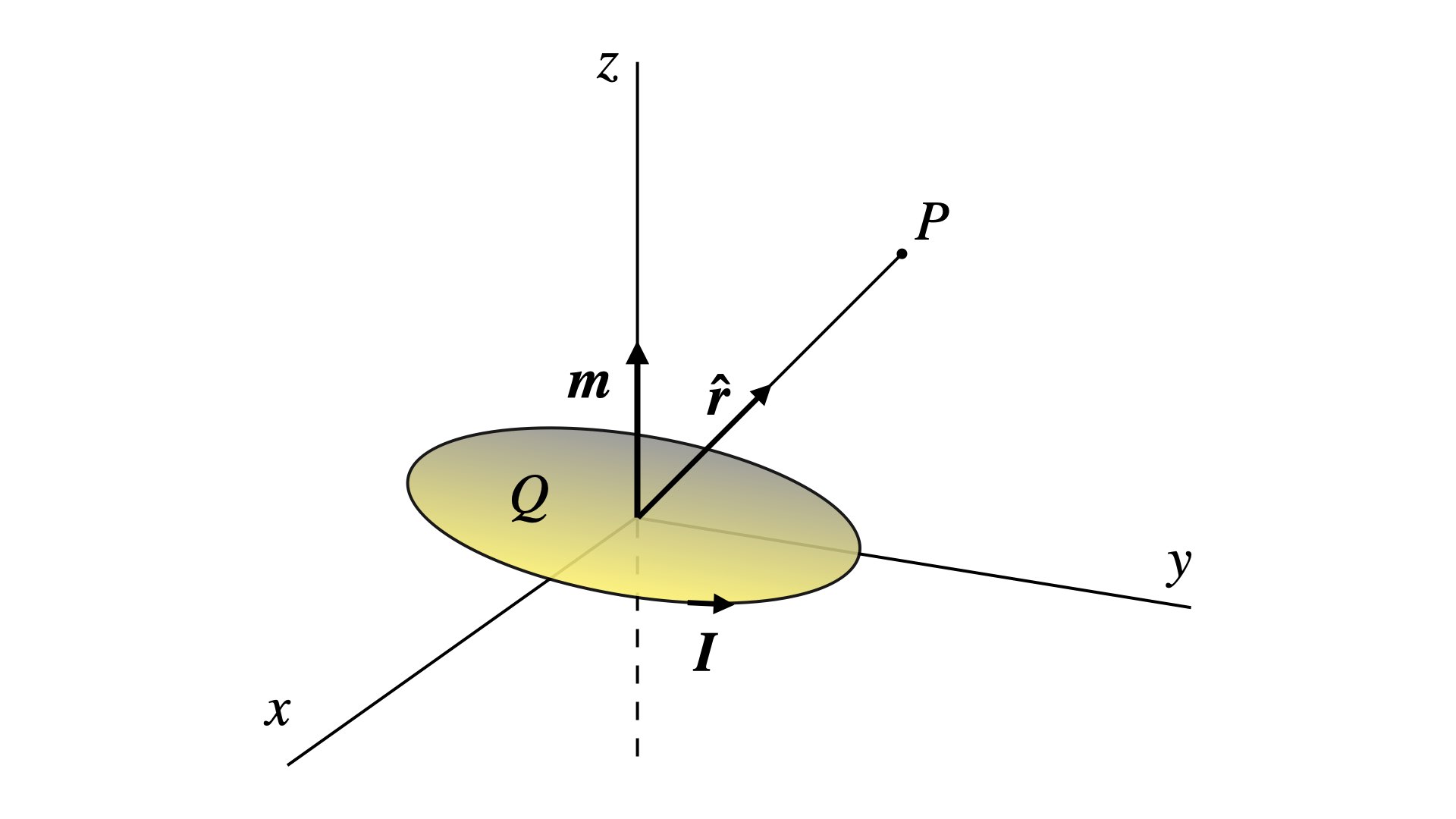
Figure 3. Modèle de dipôle magnétique formé par une petite boucle de courant.
Références
- Inspiré de Blakely, R. (1995). « Magnetic Potential », dans Potential Theory in Gravity and Magnetic Applications. Cambridge : Cambridge University Press, p. 65-80.