4.2.2 Approximation dipolaire
- Modèle de l’IGRF pour les sources internes
- La Terre : un dipôle magnétique?
- Visualisation du champ dipolaire
- Autres ressources
Modèle de l’IGRF pour les sources internes
Pour les applications de la méthode magnétique en géophysique, on va assumer que seules les sources internes du champ géomagnétique sont significatives. On peut simplifier le modèle de l’IGRF et le réécrire pour tenir compte seulement des sources internes :
\[V = a\sum_{n=1}^{\infty} \left(\frac{a}{r}\right)^{n+1} \sum_{m=0}^n (g_n^{m}\cos{m\phi} + h_n^{m}\sin{m\phi})\ P_n^m(\theta) ,\]où $a$ est le rayon de la Terre, $g$ et $h$ sont les coefficients de Gauss donnés par l’IGRF et $P_n^m$ est le polynome associé de Legendre de degré $n$ et d’ordre $m$. Cette équation correspond à une expansion multipôle du potentiel scalaire magnétique. Notez que la sommation commence maintenant à $n=1$, parce que comme on l’a vu précédemment, le terme de degré $n=0$ correspond à l’équation d’un monopôle (p. ex., le champ de gravité ou le champ électrique) et que les équations de Maxwell indiquent que les monopôles magnétiques n’existent pas.
Le terme de degré $n=1$ correspond à l’équation d’un dipôle. Notez que d’après le modèle de l’IGRF, les coefficients $g_1$ et $h_1$ (degré $n=1$) sont prédominants par rapport aux coefficients de degrés supérieurs. Ainsi, il est justifiable pour nous de vérifier si l’approximation dipolaire peut tenir la route pour le champ magnétique de la Terre.
La Terre : un dipôle magnétique?
Dans cette section, on va assumer que le champ géomagnétique est causé par un dipôle dont le moment dipolaire est $\boldsymbol{m}$. On va comparer cette approximation avec les prédictions du modèle de l’IGRF pour estimer la direction et l’amplitude de $\boldsymbol{m}$.
Approximation dipolaire
Prenons l’équation (1) et évaluons la première sommation pour le degré $n=1$ seulement (un dipôle). Le potentiel du dipôle ($V_D$) est
\[V_D = \frac{a^3}{r^2} \left[ g_1^0 P_1^0(\theta) + (g_1^1\cos\phi + h_1^1 \sin\phi) P_1^1(\theta) \right] .\]D’après le tableau des polynômes associés de Legendre, $P_1^0 = \cos\theta$ et $P_1^1 = \sin\theta$. On les substitue dans l’équation (2) pour obtenir
\[V_D = \frac{a^3}{r^2} \left[ g_1^0 \cos\theta + g_1^1\cos\phi\sin\theta + h_1^1 \sin\phi \sin\theta \right] ,\]où on reconnait la définition des coordonnées sphériques par rapport aux coordonnées cartésiennes :
\[\begin{align} x &= r\sin\theta\cos\phi \\ y &= r\sin\theta\sin\phi\\ z &= r\cos\theta. \end{align}\]L’équation (3) est donc équivalente à
\[V_D = \frac{a^3}{r^2} \left[ g_1^0\frac{z}{r} + g_1^1\frac{x}{r} + h_1^1\frac{y}{r} \right] .\]Comparaison avec le potentiel d’un dipôle
On a vu dans la section 4.1 que le potentiel d’un dipôle magnétique est
\[V = \frac{C_m}{r^2} \boldsymbol{m}\cdot\boldsymbol{\hat{r}} ,\]où $C_m = \mu_0/4\pi$. En écrivant le produit scalaire entre $\boldsymbol{m}$ et $\boldsymbol{\hat{r}}$ de façon explicite, on obtient
\[V = \frac{C_m}{r^2} \left[ m_x\frac{x}{r} + m_y\frac{y}{r} + m_z\frac{z}{r} \right] ,\]La ressemblance entre les équations (7) et (9) est frappante. Ça confirme que le fait de prendre seulement le terme en $n=1$ du modèle de l’IGRF revient à modéliser le potentiel géomagnétique avec un simple dipôle. Spécifiquement, on voit que les composantes $m_x$, $m_y$ et $m_z$ du moment dipolaire sont directement proportionnelles aux coefficients de Gauss $g_1^1$, $g_h^1$ et $g_1^0$, respectivement, tel que
\[\begin{align} m_x &= \frac{4\pi}{\mu_0} a^3 g_1^1\\ m_y &= \frac{4\pi}{\mu_0} a^3 h_1^1\\ m_z &= \frac{4\pi}{\mu_0} a^3 g_1^0. \end{align}\]Estimation du moment magnétique interne
D’après le tableau des coefficients de Gauss de 2020,
\[\begin{align} g_1^1 &= -1450.9\ \text{nT}\\ h_1^1 &= 4652.5\ \text{nT}\\ g_1^0 &= -29404.8\ \text{nT}, \end{align}\]et en utilisant un rayon de la Terre moyen de $a = 6371$ km, on obtient que
\[\begin{align} m_x &= -3.752\times 10^{21}\ \text{A m}^2\\ m_y &= 1.203\times 10^{22}\ \text{A m}^2\\ m_z &= 7.604\times 10^{22}\ \text{A m}^2. \end{align}\]Ces informations nous permettent de calculer la magnitude du moment magnétique de l’approximation dipolaire, ce qui donne
\[\begin{align} m &= \sqrt{m_x^2 + m_y^2 + m_z^2}\\ & = 7.708\times 10^{22}\ \text{A m}^2. \end{align}\]Ces nombres sont très grands ($10^{22}$) et difficiles à concevoir. À titre comparatif, un aimant de néodyme fer-bore de la taille d’une boule de quille a un moment magnétique de 5937 $\text{A m}^2$. Un disque composé du même matériau, mais de la taille d’une pièce de 1 cent a un moment magnétique de 0.4824 $\text{A m}^2$, alors que le disque de néodyme bore-fer dans un téléphone portable typique a un moment magnétique de 0.007909 $\text{A m}^2$ (source). Il faut en conclure que la Terre est un aimant extrêmement puissant.
On peut utiliser les composantes de $m$ trouvées pour déterminer quel serait la colatitude ($\theta$) et la longitude ($\phi$) de l’orientation du dipôle s’il était situé au centre de la Terre :
\[\theta = \arccos\frac{m_z}{m} = 9.41^{\circ} ,\]et
\[\phi = \arccos\frac{m_x}{\sqrt{m_x^2 + m_y^2}} = 107.32^{\circ}.\]Pôles magnétiques
Il faut différencier deux types de pôles magnétiques.
Les pôles magnétiques sont l’endroit sur Terre où le champ magnétique est complètement vertical. C’est-à-dire qu’au pôle Nord magnétique, l’aiguille d’une boussole pointe directement vers le bas. Au pôle Sud magnétique, l’aiguille d’une boussole pointe directement vers le haut.
Les pôles géomagnétiques sont l’endroit où le vecteur de l’approximation du dipôle magnétique intersecte la surface terrestre. En prolongeant l’orientation du dipôle trouvée plus haut, on trouve que le pôle Sud géomagnétique est situé aux coordonnées 80.59°S 107.32°E. Conséquemment le pôle Nord géomagnétique se trouve aux coordonnées 80.59°N 72.68°O.
La différence d’emplacement entre les pôles magnétiques et géomagnétiques (Figure 1) vient de l’approximation dipolaire du champ géomagnétique. Il est possible de montrer que la composante «non dipolaire» du champ représente environ 10 % du total. L’approximation dipolaire reste donc une excellente approximation.
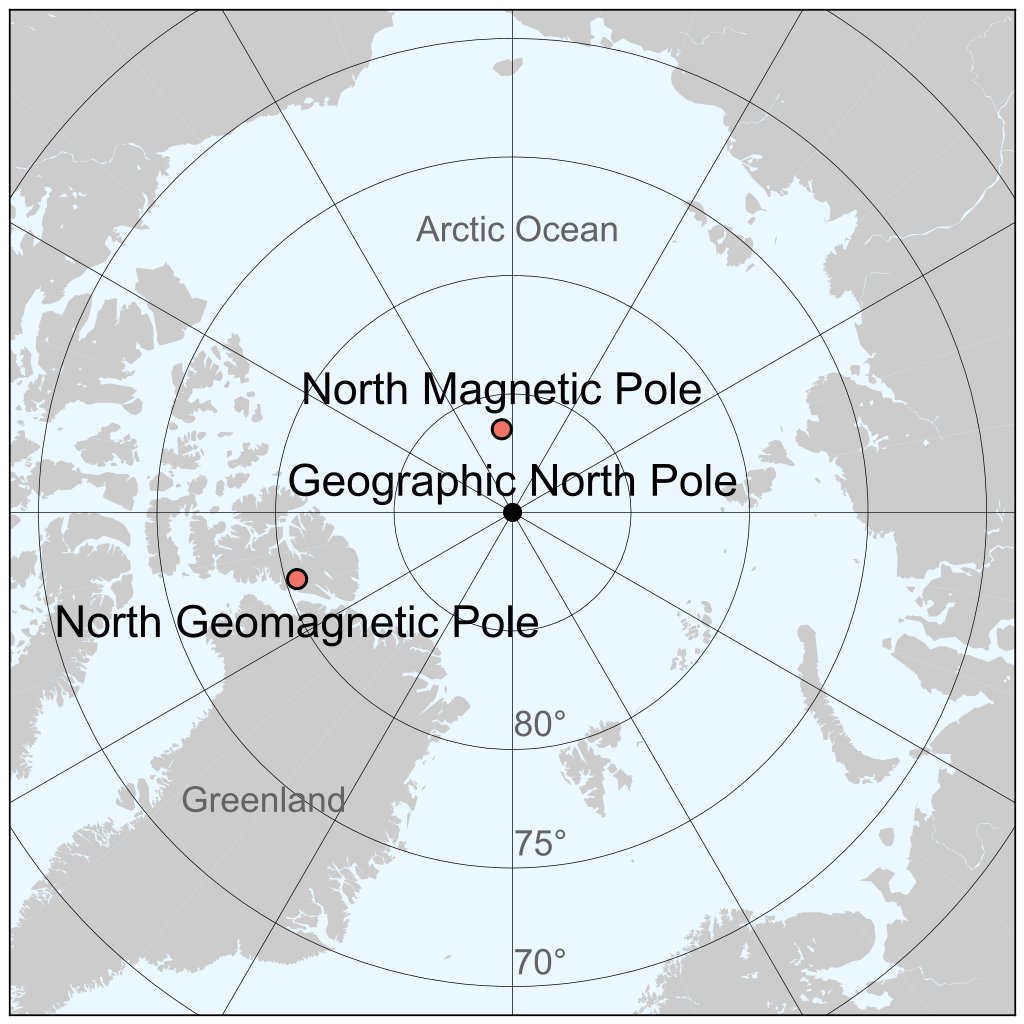
Figure 1. Emplacement des pôles Nord géographiques, magnétiques et géomagnétiques en 2017. Image par Cavit.
Visualisation du champ dipolaire
On peut maintenant utiliser ce qu’on a appris dans le chapitre 4 pour voir les lignes du champ magnétique dipolaire de la Terre avec Python. Le résultat est montré à la Figure 2.
Figure 2. Visualisation du champ magnétique dipolaire.
Comme on peut le voir, d’après le modèle du dipôle terrestre, les lignes de champs sont la prolongation du dipôle qui pointe vers le pôle Sud géomagnétique. Les lignes de champ font une boucle et reviennent au pôle Nord géomagnétique. Près de l’équateur, le champ est donc surtout horizontal ($T \approx B_x$). Près des pôles, le champ est presque vertical ($T \approx B_z$).
Autres ressources
- Lire la page sur les modèles de référence du champ magnétique de Ressources naturelles Canada