4.4.1 Réduction au pôle et à l’équateur

• Définitions intuitives
  • Réduction au pôle
  • Réduction à l’équateur
  • Opération dans le domaine spectral
• Formulation mathématique
  • Vecteurs unitaires
  • Anomalies magnétiques dans le domaine spectral
  • Anomalie réduite
• Dérivation de la réduction au pôle
• Dérivation de la réduction à l’équateur
• Résumé
  • Formules importantes
  • Implémentation en Python
• Références

---

Définitions intuitives

Réduction au pôle

Les anomalies de champ total sont asymétriques lorsque le champ externe ($\boldsymbol{F}$) est incliné par rapport à la verticale, c’est-à-dire lorsque $I \neq 90^{\circ}$ ou $I \neq -90^{\circ}$. La réduction au pôle est une opération de filtrage qui vise à redresser les anomalies pour les rendre symétriques, en effectuant une rotation du champ externe vers la verticale. Le résultat est une représentation de l’anomalie de champ total ($\Delta T$), comme si celle-ci avait été mesurée au pôle Nord magnétique au lieu d’une latitude quelconque. Conséquemment l’anomalie devient plus facile à interpréter grâce à sa symétrie. La Figure 1 montre un exemple d’une anomalie de champ total avant et après l’opération de réduction au pôle.

Figure 1. Profils d’anomalies de champ total créées par un dipôle magnétique avant et après des opérations de réduction au pôle et à l’équateur. Avant les opérations, l’inclinaison du champ externe primaire était $45^{\circ}$, sa déclinaison $0^{\circ}$ et son intensité 55 000 nT.

Réduction à l’équateur

La réduction à l’équateur est semblable à la réduction au pôle, mais comme son nom l’indique, elle vise à filtrer les anomalies pour les représenter comme si elles avaient été mesurées à l’équateur magnétique. On utilise rarement la réduction à l’équateur pour traiter les données d’un levé magnétique sauf si celui-ci à été réalisé près de l’équateur. La raison est que la réduction au pôle devient instable quand on tente de l’appliquer à des données prises où le champ externe est presque horizontal ; on se rabat donc sur une réduction à l’équateur, qui est une opération stable dans ce cas. L’opposé est aussi vrai : la réduction à l’équateur pour des données aquises près des pôles magnétiques sera instable. Au Québec, où la latitude est généralement plus élevée que $45^{\circ}$, la réduction au pôle est l’opération la plus stable et appropriée pour réduire les anomalies à une forme symétrique.

Opération dans le domaine spectral

Les réductions au pôle et à l’équateur sont des opérations qu’on peut faire dans le domaine spectral. Le principe d’application est très semblable à celui du prolongement vers le haut ou du calcul des dérivées spatiales, par exemple. La recette reste donc sensiblement la même :

1. Calculer la transformation de Fourier du signal original
2. La multiplier avec le filtre spectral de réduction au pôle ou à l’équateur
3. Calculer la transformation de Fourier inverse du résultat

---

Formulation mathématique

On sait que l’anomalie de champ total ($\Delta T$) est donnée par

\[\begin{equation*} \Delta T \approx \boldsymbol{\hat{F}} \cdot \boldsymbol{\Delta F} , \end{equation*}\]

où $\boldsymbol{\Delta F}$ est une perturbation dans le champ régional ($\boldsymbol{F}$) causée par des contrastes de susceptibilité magnétique dans la géologie.

Vecteurs unitaires

Les réductions au pôle et à l’équateur sont des opérations de rotation, il sera utile de bien comprendre la direction des vecteurs de l’aimantation et du champ primaire. On va dénoter $\boldsymbol{\hat{f}}$ et $\boldsymbol{\hat{m}}$ comme les vecteurs unitaires qui pointent dans les directions du champ primaire et de l’aimantation, respectivement. Conséquemment, pour le champ primaire,

\[\begin{equation*} \boldsymbol{\hat{f}} = \begin{pmatrix} \hat{f}_x\\ \hat{f}_y\\ \hat{f}_z \end{pmatrix} = \begin{pmatrix} \cos(I)\cos(D)\\ \cos(I)\sin(D)\\ \sin(I) \end{pmatrix}, \end{equation*}\]

où $I$ est l’inclinaison du champ primaire et $D$ est sa déclinaison. On appelle les composantes d’un vecteur unitaire les cosinus directeurs (Figure 2).

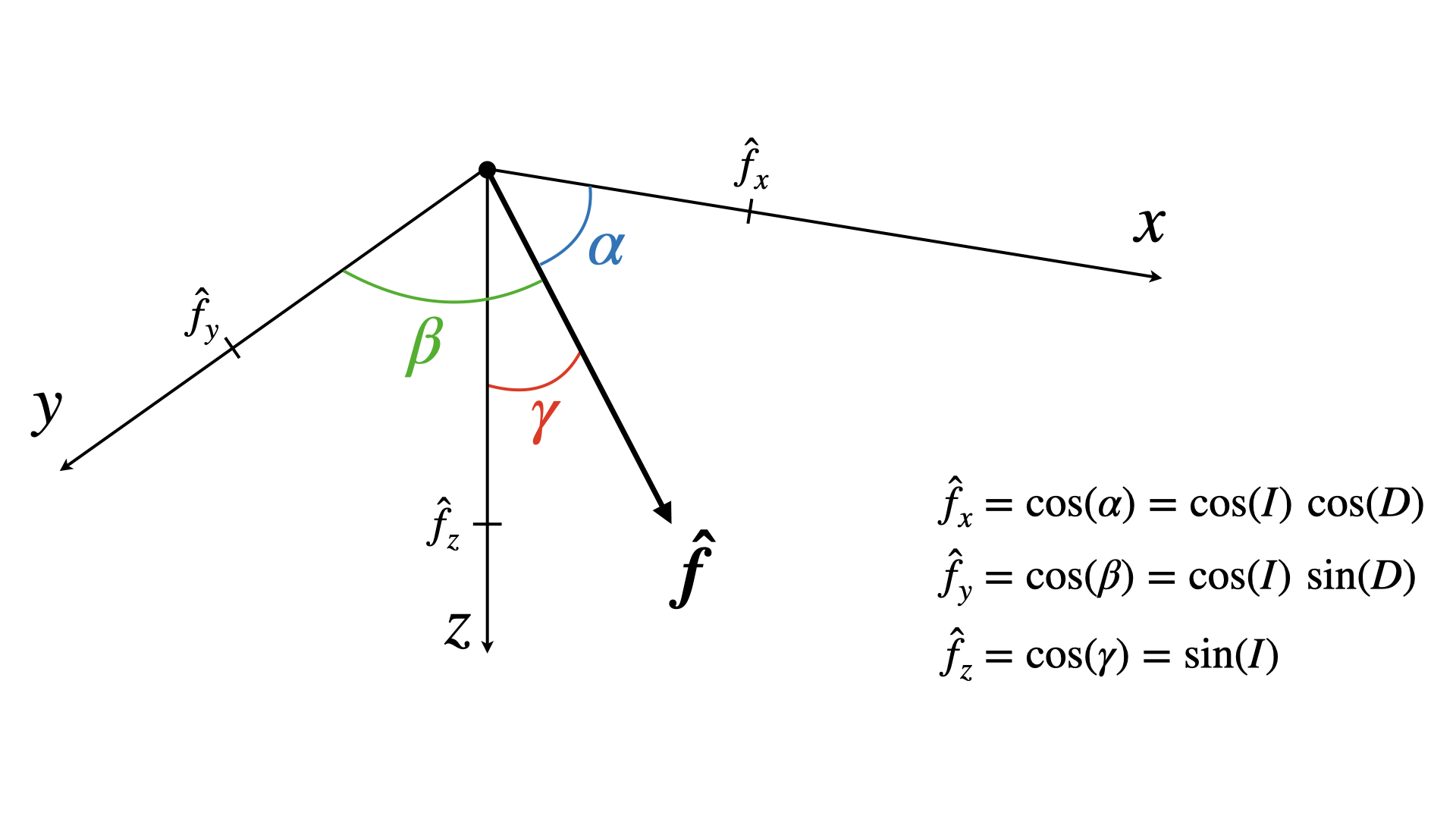
Figure 2. Schéma montrant les cosinus directeurs ($\alpha$, $\beta$, $\gamma$) du vecteur unitaire $\boldsymbol{\hat{f}}$. En géomagnétisme l’axe des $z$ est défini comme positif vers le bas, l’axe des $x$ est positif vers le Nord et l’axe des $y$ est positif vers l’Est. Les cosinus directeurs peuvent s’écrire en fonction des paramètres d’inclinaison et de déclinaison du champ magnétique.

S’il n’y a pas d’aimantation rémanente (toute l’aimantation est dans la même direction que le champ primaire), alors $\boldsymbol{\hat{m}}$ pointe dans la même direction que $\boldsymbol{\hat{f}}$ et

\[\begin{equation*} \boldsymbol{\hat{m}} = \begin{pmatrix} \hat{m}_x\\ \hat{m}_y\\ \hat{m}_z \end{pmatrix} = \begin{pmatrix} \cos(I)\cos(D)\\ \cos(I)\sin(D)\\ \sin(I) \end{pmatrix}. \end{equation*}\]

S’il y a une aimantation rémanente dans le matériau, alors il faut définir $\boldsymbol{\hat{m}}$ selon sa direction.

Anomalies magnétiques dans le domaine spectral

La transformation de Fourier ($\mathcal{F}$) de l’anomalie mesurée vers le domaine spectral donne [1]:

\[\begin{equation*} \mathcal{F}(\Delta T) = \Theta_m(k)\ \Theta_f(k)\ S(k) , \tag{1} \end{equation*}\]

où $\Theta_m$ et $\Theta_f$ sont respectivement les transformations de Fourier des facteur dus à la direction de l’aimantation dans le matériau et à la direction du champ primaire. $S$ est un terme qui décrit le contenu fréquentiel du signal et $k$ sont les indices des fréquences spatiales.

En coordonnées cartésiennes (3D):

\[\begin{equation*} \Theta_m = \hat{m}_z + i \left(\frac{\hat{m}_x k_x + \hat{m}_y k_y}{\vert k \vert}\right) \tag{2} \end{equation*}\]

et

\[\begin{equation*} \Theta_f = \hat{f}_z + i \left(\frac{\hat{f}_x k_x + \hat{f}_y k_y}{\vert k \vert}\right) , \tag{3} \end{equation*}\]

où $i$ est le nombre imaginaire ($i^2 = −1$).

Anomalie réduite

On cherche maintenant l’anomalie réduite (celle obtenue après une opération de réduction au pôle ou à l’équateur). On dénotera l’anomalie réduite par $\Delta T’$. La transformation de Fourier de l’anomalie réduite est

\[\begin{equation*} \mathcal{F}(\Delta T') = \Theta_m'(k)\ \Theta_f'(k)\ S(k) , \tag{4} \end{equation*}\]

où $\Theta_m’(k)$ et $\Theta_f’(k)$ sont les transformation de Fourier des facteurs dus aux nouvelles directions de l’aimantation et du champ primaire après la réduction. Ici, $S(k)$ doit être le même que dans l’équation (1), car l’opération de réduction doit préserver le contenu fréquentiel du signal. En combinant (1) et (4), on obtient

\[\begin{equation*} \frac{\mathcal{F}(\Delta T)}{\Theta_m\Theta_f} = \frac{\mathcal{F}(\Delta T')}{\Theta_m'\Theta_f'} , \end{equation*}\]

et donc

\[\begin{equation*} \mathcal{F}(\Delta T') = \frac{\Theta_m'\Theta_f'}{\Theta_m\Theta_f} \mathcal{F}(\Delta T) . \tag{5} \end{equation*}\]

L’équation (5) est la formule générale pour une rotation de l’anomalie de champ total dans le domaine spectral. Dans ce qui suit, on utilisera $\Delta T’ = \Delta T_{p}$ pour une anomalie réduite au pôle et $\Delta T’ = \Delta T_{e}$ pour une anomalie réduite à l’équateur.

---

Dérivation de la réduction au pôle

On sait qu’au pôle Nord magnétique, le champ primaire pointe directement vers le bas ($I = 90^{\circ}$). En absence d’aimantation rémanente ça veut aussi dire que les moments dipolaires des corps ayant une susceptibilité magnétique s’alignent avec le champ primaire, soit vers le bas. En termes des vecteurs unitaires $\boldsymbol{\hat{f}}’$ et $\boldsymbol{\hat{m}}’$ décrivant l’anomalie réduite, ça veut dire que tout pointe dans la direction $\boldsymbol{\hat{z}}$ :

\[\begin{equation*} \boldsymbol{\hat{f}'} = \boldsymbol{\hat{m}'} = \begin{pmatrix} \hat{f}_x'\\ \hat{f}_y'\\ \hat{f}_z' \end{pmatrix} = \begin{pmatrix} \hat{m}_x'\\ \hat{m}_y'\\ \hat{m}_z' \end{pmatrix} = \begin{pmatrix} 0\\ 0\\ 1 \end{pmatrix}. \end{equation*}\]

Il en découle que

\[\begin{equation*} \hat{f}_z' = \hat{m}_z' = 1 \end{equation*}\]

et

\[\begin{equation*} \Theta_m' = \Theta_f' = 1 , \end{equation*}\]

donc

\[\begin{equation*} {\Theta_m'\Theta_f'} = 1 . \end{equation*}\]

La transformation de Fourier de l’anomalie réduite au pôle devient :

\[\begin{equation*} \mathcal{F}(\Delta T_{p}) = \frac{1}{\Theta_m\Theta_f} \mathcal{F}(\Delta T). \end{equation*}\]

Si on définit le terme $\Theta_f$ en fonction des cosinus directeurs :

\[\begin{align*} \Theta_f & = \sin(I) + \frac{ik_x \cos(I) \cos(D)}{\vert k \vert} + \frac{ik_y \cos(I) \sin(D)}{\vert k \vert} \\ & = \sin(I) + i\cos(I) \left[ \frac{k_x \cos(D)}{\sqrt{k_x^2 + k_y^2}} + \frac{k_y \sin(D)}{\sqrt{k_x^2 + k_y^2}} \right]. \\ \tag{6} \end{align*}\]

On va maintenant simplifier l’équation à l’aide d’une substitution de variable, soit

\[\begin{equation*} \mu = \arctan\left(\frac{k_y}{k_x}\right) \end{equation*}\]

et d’une identité trigonométrique qui dit que

\[\begin{align*} \cos(D - \mu) & = \sin(\mu)\sin(D) + \cos(\mu)\cos(D) \\ & = \frac{k_y}{\sqrt{k_x^2 + k_y^2}}\sin(D) + \frac{k_x}{\sqrt{k_x^2 + k_y^2}}\cos(D). \end{align*}\]

On remarque que ces termes sont présents dans l’équation de $\Theta_f$ (6). On trouve que

\[\begin{equation*} \Theta_f = \sin(I) + i\cos(I)\cos(D- \mu) \end{equation*}\]

Dans le cas où il n’y a pas d’aimantation rémanente, on sait que $\Theta_m = \Theta_f$. L’équation (5) pour une réduction au pôle est finalement

\[\begin{equation*} \mathcal{F}(\Delta T_{p}) = \left[\frac{1}{(\sin(I) + i\cos(I)\cos(D- \mu)}\right]^2\ \mathcal{F}(\Delta T). \tag{7} \label{eq:redpole} \end{equation*}\]

---

Dérivation de la réduction à l’équateur

La dérivation de la formule de réduction des anomalies magnétiques à l’équateur suit le même raisonnement que celle de la réduction au pôle. La différence est qu’à l’équateur magnétique, on s’attend à avoir un champ primaire qui est complètement horizontal et pointe vers le Nord magnétique. En termes des vecteurs unitaires $\boldsymbol{\hat{f}}’$ et $\boldsymbol{\hat{m}}’$ après la réduction, ça veut dire que tout pointe dans la direction $\boldsymbol{\hat{x}}$ :

\[\begin{equation*} \boldsymbol{\hat{f}'} = \boldsymbol{\hat{m}'} = \begin{pmatrix} \hat{f}_x'\\ \hat{f}_y'\\ \hat{f}_z' \end{pmatrix} = \begin{pmatrix} \hat{m}_x'\\ \hat{m}_y'\\ \hat{m}_z' \end{pmatrix} = \begin{pmatrix} 1\\ 0\\ 0 \end{pmatrix}. \end{equation*}\]

De là, on obtient lorsqu’il n’y a pas d’aimantation rémanente que

\[\begin{equation*} \Theta_m' = \Theta_f' = i\hat{m}_x\frac{k_x}{\vert k \vert} \end{equation*}\]

et donc

\[\begin{align*} \Theta_m'\Theta_f' & = -\hat{m}_x^2\frac{k_x^2}{k_x^2 + k_y^2} \\ & = -\frac{k_x^2}{k_x^2 + k_y^2} \\ & = -\frac{1}{1 + \left(\frac{k_y}{k_x}\right)^2} \\ & = -\frac{1}{1 + \tan^2(\mu)} \\ & = -\frac{1}{\sec^2(\mu)} \\ & = -\cos^2(\mu). \\ \end{align*}\]

L’équation (5) pour une réduction à l’équateur est finalement

\[\begin{equation*} \mathcal{F}(\Delta T_{e}) = -\left[\frac{\cos(\mu)}{(\sin(I) + i\cos(I)\cos(D-\mu)}\right]^2\ \mathcal{F}(\Delta T) . \tag{7} \label{eq:redeq} \end{equation*}\]

---

Résumé

Formules importantes

Pour résumer, la réduction au pôle d’une anomalie magnétique de champ total est donnée par

\[\begin{equation*} \Delta T_{p} = \mathcal{F}^{-1} \left\{ \psi_p\ \mathcal{F}(\Delta T) \right\} \tag{8} \end{equation*}\]

et sa réduction à l’équateur est donnée par

\[\begin{equation*} \Delta T_{e} = \mathcal{F}^{-1} \left\{ \psi_e\ \mathcal{F}(\Delta T) \right\}. \tag{9} \end{equation*}\]

Dans l’équation (8), $\psi_p$ est l’opérateur de filtrage pour la réduction au pôle dans le domaine spectral :

\[\begin{equation*} \psi_p = \left[ \sin(I) + i\cos(I)\cos(D-\mu)\right]^{-2}. \tag{10} \end{equation*}\]

Dans l’équation (9) $\psi_e$ est l’opérateur de filtrage pour la réduction à l’équateur dans le domaine spectral :

\[\begin{equation*} \psi_e = -\cos^2(\mu)\ \psi_p .\tag{11} \end{equation*}\]

La variable de substitution

\[\begin{equation*} \mu = \arctan\left(\frac{k_y}{k_x}\right) \end{equation*}\]

dépend des fréquences spatiales $k_x$ et $k_y$ associées à la transformation de Fourier de l’anomalie originale.

Implémentation en Python

La dérivation faite dans cette section peut sembler compliquée à première vue. Cependant l’implémentation de la réduction au pôle reste relativement simple dans les languages de programmation modernes. Par exemple, en Python, on utiliserait une fonction similaire à :

import numpy as np

def reduction_pole(T, I, D, step):
    """Calcule le prolongement du champ `gz` à une hauteur `h`.
    Args:
        T (2d array): Anomalie de champ total (m x n).
        I (float): Inclinaison du champ en degrés.
        D (float): Déclinaison du champ en degrés.
        step (tuple): Pas (x, y) entre les stations en mètres.
    Returns:
        (2d array): L'anomalie réduite au pôle.
    """
    I_rad, D_rad = np.radians(I), np.radians(D)  # conversion en radians
    T_hat = np.fft.fft2(T)  # transformation Fourier
    k_x = np.fft.fftfreq(n=T.shape[0], d=step[0])  # calcul kx
    k_y = np.fft.fftfreq(n=T.shape[1], d=step[1])  # calcul ky
    KXX, KYY = np.meshgrid(k_x, k_y)  # mettre kx et ky en grille
    mu = np.arctan2(KYY, KXX)
    psi = (np.sin(I_rad) + 1j*np.cos(I_rad)*np.cos(D_rad - mu))**-2 
    T_hat *=  psi  # filtrage
    T_pole = np.fft.ifft2(T_hat).real  # transformation inverse
    return T_pole

Prenez le temps de bien comprendre chaque étape effectuée dans la fonction.

---

Références

Blakely, R. (1995). Transformations. Dans Potential Theory in Gravity and Magnetic Applications (pp. 311-358). Cambridge: Cambridge University Press.