4.1.5 Champ magnétique dipolaire
Rappels
Pour trouver la densité de flux magnétique d’un dipôle, il faut faire appel à deux notions qu’on a vu dans la section précédente.
Champ conservatif
On sait que la densité de flux magnétique (le champ $\boldsymbol{B}$) peut s’exprimer comme le gradient d’un potentiel scalaire ($V$), tel que
\[\boldsymbol{B} = -\nabla V ,\]où $\boldsymbol{B} = B_r\ \boldsymbol{\hat{r}} + B_{\theta}\ \boldsymbol{\hat{\theta}} + B_{\phi}\ \boldsymbol{\hat{\phi}}$ en coordonnées sphériques, par exemple.
Potentiel d’un dipôle
Dans la section prédécente, on a montré que le potentiel ($V$) d’un dipôle magnétique à un point d’observation $P$ est
\[V(P) = -C_m \boldsymbol{m} \cdot \nabla \frac{1}{r} ,\]où $C_m = \mu_0/4\pi = 10^{-7}$ $\textrm{NA}^{-2}$ est une constante, $\nabla$ est l’opérateur différentiel vectoriel, $\boldsymbol{m}$ est le vecteur du moment dipolaire magnétique et $r$ est la distance radiale entre le dipôle et $P$.
En coordonnées sphériques, par exemple, le potentiel est tout simplement
\[V(P) = \frac{C_m}{r^2} \boldsymbol{m}\cdot\boldsymbol{\hat{r}} .\]Calcul du champ dipolaire
Coordonnées sphériques
Dans un système de coordonnées sphériques, pour un dipôle placé à l’origine et qui pointe dans la direction $\boldsymbol{\hat{z}}$, on a que $\boldsymbol{m}\cdot\boldsymbol{\hat{r}} = m \cos\theta$ (Figure 1).
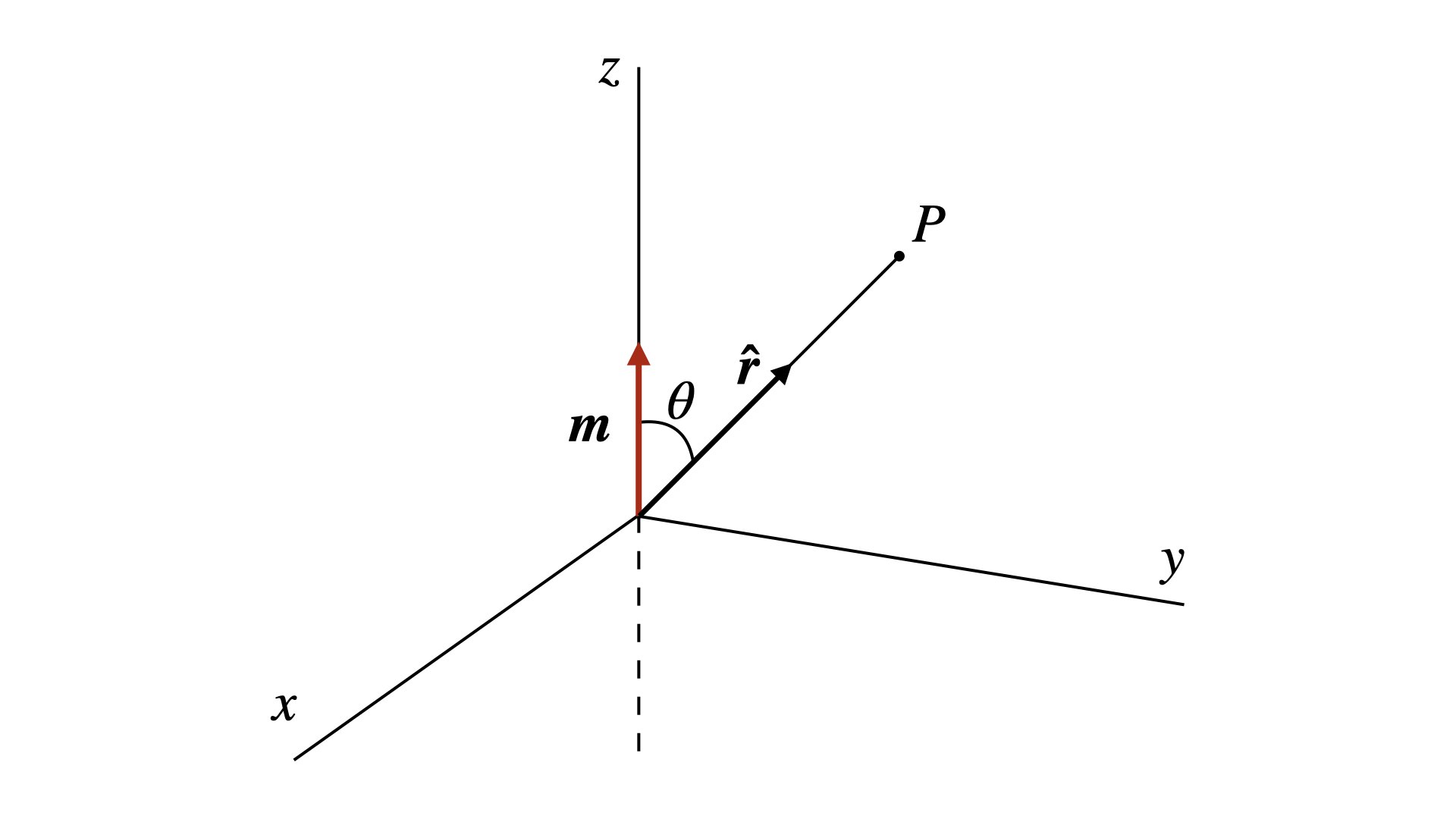
Figure 1. Schéma montrant un dipôle magnétique situé à l’origine.
Donc le potentiel s’écrit comme
\[V(P) = \frac{C_m}{r^2} m\cos\theta .\]On peut utiliser l’équation (1) pour calculer chaque composante individuelle du champ $\boldsymbol{B}$ :
\[\begin{align} B_r = -\frac{\partial V}{\partial r} = \frac{2C_m}{r^3} m\cos\theta, \end{align}\] \[\begin{align} B_{\theta} = -\frac{1}{r}\frac{\partial V}{\partial \theta} = \frac{C_m}{r^3} m\sin\theta, \end{align}\]et
\[\begin{align} B_{\phi} = -\frac{1}{r\sin\theta}\frac{\partial V}{\partial \phi} = 0. \end{align}\]Finalement, on obtient $\boldsymbol{B}$ avec
\[\boldsymbol{B} = \frac{C_m}{r^3} \left[ 2m\cos\theta\ \boldsymbol{\hat{r}} + m\sin\theta\ \boldsymbol{\hat{\theta}} \right] .\]Formulation générale
Il est possible d’écrire cette équation de façon indépendante du système de coordonnées, ce qui est pratique quand la géométrie du problème devient plus complexe. On sait que
\[\begin{align} \boldsymbol{m} &= (\boldsymbol{m}\cdot\boldsymbol{\hat{r}})\ \boldsymbol{\hat{r}} + (\boldsymbol{m}\cdot\boldsymbol{\hat{\theta}})\ \boldsymbol{\hat{\theta}} \\ &= m\cos\theta\ \boldsymbol{\hat{r}} - m\sin\theta\ \boldsymbol{\hat{\theta}}. \end{align}\]Il en découle que
\[\begin{align} 3(\boldsymbol{m}\cdot\boldsymbol{\hat{r}})\ \boldsymbol{\hat{r}} - \boldsymbol{m} &= 3m\cos\theta\ \boldsymbol{\hat{r}} - m\cos\theta\ \boldsymbol{\hat{r}} + m\sin\theta\ \boldsymbol{\hat{\theta}}\\ &= 2m\cos\theta\ \boldsymbol{\hat{r}} + m\sin\theta\ \boldsymbol{\hat{\theta}}. \end{align}\]On reconnait cette forme dans l’équation de $\boldsymbol{B}$. Ça veut dire qu’on peut écrire $\boldsymbol{B}$ dans une forme indépendante du système de coordonnées avec
\[\boldsymbol{B} = C_m\frac{m}{r^3} \left[3(\boldsymbol{\hat{m}}\cdot\boldsymbol{\hat{r}})\ \boldsymbol{\hat{r}} - \boldsymbol{\hat{m}}\right] .\]Exemple : visualiser le champ magnétique
Il est important de visualiser le champ $\boldsymbol{B}$ pour comprendre comment il diffère d’un champ purement radial, comme celui de la gravité. En effet, vous venez de découvrir d’après l’équation (8) que $\boldsymbol{B}$ a non seulement une composante radiale, mais aussi une composante tangentielle!
On va utiliser Python pour tracer les lignes du champ $\boldsymbol{B}$. Comme d’habitude on commence par importer les modules nécessaires.
import numpy as np
import matplotlib.pyplot as plt
Ensuite on définit une fonction qui permettra de calculer $\boldsymbol{B}$ pour une série de coordonnées ($r$, $\theta$).
def B(r, theta):
"""Calcule le champ magnétique à (r, theta)."""
Cm = 1e-7 # égal à mu_0 / 4 pi
m = 1 # on normalise par m pour simplifier
facteur = Cm*(m/r**3)
return 2*facteur*np.cos(theta), facteur*np.sin(theta)
Puis on définit une grille sur laquelle $\boldsymbol{B}$ sera calculé.
# Grille cartésienne de points (x, y)
nx, ny = 50, 50 # nombre de points en x, y
XMAX, YMAX = 100, 60 # distances maximales du centre (arbitraire)
x = np.linspace(-XMAX, XMAX, nx)
y = np.linspace(-YMAX, YMAX, ny)
X, Y = np.meshgrid(x, y)
r, theta = np.hypot(X, Y), np.arctan2(Y, X) # en coordonnées polaires
Il ne reste qu’à passer cette grille à la fonction définie précédemment.
B_r, B_theta = B(r, theta)
En vous épargnant les détails de la mise en graphique, le résultat est montré à la Figure 2.
Figure 2. Schéma montrant la densité de flux magnétique générée par un dipôle magnétique situé à l’origine.
La Figure 2 montre que le champ $\boldsymbol{B}$ d’un dipôle magnétique est comme celui qui serait produit par un petit aimant. Celui-ci varie en $1/r^3$, ce qui est représenté par le changement de couleur sur les lignes de champ. À la source (à l’origine) $\boldsymbol{B}$ est parallèle à $\boldsymbol{m}$ et va dans la même direction. Puis, les lignes de champ font une boucle pour retourner à l’origine. Les équipotentielles seraient perpendiculaires aux lignes de champ partout.
Références
- Griffiths, D. J. (2017). « Potentials », dans Introduction to Electrodynamics, Cambridge : Cambridge University Press, p. 113–166.