1.2 Densité
- Définition
- Comment mesurer la densité
- Qu’est-ce qui détermine la densité d’une roche?
- Valeurs typiques de la densité
- Profil de densité de la Terre
- Autres ressources
Définition
La masse volumique des matériaux (dénotée $\rho$) est le rapport entre leur masse $m$ contenue par unité de volume $V$, tel que
\[\begin{equation} \rho = \frac{m}{V}. \end{equation}\]Strictement parlant, la densité d’un matériau est le rapport entre la masse volumique de celui-ci et celle de l’eau à 4°C. La densité n’aurait donc pas de dimensions.
Cependant, la litérature géophysique utilise souvent à tort le terme «densité» pour faire référence à la masse volumique, ou la densité volumique de masse. Il s’agit d’un léger abus de langage qu’on va tolérer en géophysique.
Cette confusion vient du fait que le mot anglais pour masse volumique est density, alors que le mot anglais pour densité est relative density ou encore specific gravity. Dans le langage géophysique courant, les termes densité et masse volumique représentent effectivement la même chose parce que la densité de l’eau ($\rho_{w}$) à 4°C est environ 1 g/cm$^3$ (999.972 kg/m$^3$ pour être précis).
Dans ce cours, on suivra les conventions géophysiques et on utilisera le mot densité au sens général comme un alias pour faire référence à la masse volumique. Pour résumer :
| Formule | Unités CGS | Unités SI | |
|---|---|---|---|
| Densité (masse volumique) | $\rho=\frac{m}{V}$ | g/cm$^3$ | kg/m$^3$ |
| Densité (specific gravity) | S.G. $=\frac{\rho}{\rho_{w}}$ |
Il est important de distinguer deux types de densité pour les matériaux, soient leur densité apparente et leur densité squelettique. Une illustration simplifiée d’une section de matériau poreux est présentée à la Figure 1, où les indices $g$ et $i$ correspondent respectivement aux propriétés des grains (en gris) et au fluide interstitiel (en bleu).
Figure 1. Schéma d’un matériau poreux dont la densité des grains est $\rho_g$ et la densité du fluide interstitiel est $\rho_i$.
Densité apparente
La densité apparente ($\rho_{a}$) tient compte de toutes les composantes du matériau, incluant sa porosité et la densité de ses fluides interstitiels. La densité apparente d’un échantillon correspond à la densité des grains pondérée par rapport à la porosité de l’échantillon et la densité du fluide. Si on suppose que le matériau de la Figure 1 est complètement saturé (tous les pores sont occupés), sa densité apparente s’écrit :
\[\begin{align} \rho_a & = \frac{m_g + m_i}{V_g + V_i} \\ & = \frac{m_{totale}}{V_{total}}. \end{align}\]Densité squelettique
La densité squelettique ($\rho_{s}$) ne tient compte que des grains qui composent le matériau, excluant sa porosité et la densité de ses fluides interstitiels. En se référant toujours à la Figure 1, la densité squelettique est :
\[\begin{equation} \rho_s = \frac{m_g}{V_g}. \end{equation}\]Porosité
La porosité (souvent dénotée $\varphi$) d’un matériau est définie par le rapport entre le volume de ses pores et son volume total :
\[\begin{equation} \varphi = \frac{V_i}{V_{total}}. \end{equation}\]Comment mesurer la densité
Il existe différentes méthodes pour mesurer la densité. Les principaux avantages et inconvénients des différentes méthodes pour mesurer la densité sont résumés dans le tableau suivant :
| Méthode | Avantages | Inconvénients |
|---|---|---|
| En vrac | Simple, géométries variables | Faible précision |
| Archimède | Précis jusqu’à 1 kg/m$^3$ | Matériaux consolidés seulement |
| Pycnomètre | Matériaux consolidés ou non | Petits volumes seulement |
| Nucléodensimètre | Mesures en forage | Manipulations complexes |
Méthode en vrac
La méthode en vrac ne tient pas compte de la porosité des matériaux. Elle consiste à peser un échantillon avec une balance à haute précision pour obtenir sa masse $m$, puis d’observer le volume d’eau déplacé lorsque l’échantillon est submergé. La densité est obtenue avec la relation $\rho = m/V$. Cette méthode permet d’obtenir des résultats rapides, mais elle est généralement peu précise parce qu’il est difficile d’obtenir une bonne précision sur le volume d’eau déplacé avec un cylindre gradué. La méthode en vrac donne la densité apparente de l’échantillon, elle ne tient pas compte des espaces vides qui forment sa porosité. On considère que cette méthode ne donne pas des résultats assez précis pour la plupart des applications pratiques en géophysique.
Méthode d’Archimède
La méthode d’Archimède, aussi appelée méthode de pesée hydrostatique, consiste à obtenir la densité d’un échantillon de matériau en comparant sa masse réelle ($m$) avec sa masse apparente dans l’eau ($m_{a}$). Souvenez-vous, le principe d’Archimède veut qu’une force de bouée agisse vers le haut sur un corps de masse $m$ lorsque celui-ci est submergé dans l’eau. La différence entre la masse réelle et la masse apparente est donc égale à la masse d’eau déplacée ($m_w$), alors
\[\begin{equation*} m - m_a = m_w = \rho_w V, \end{equation*}\]où $V = m/\rho$ est le volume d’eau déplacé par l’échantillon. La densité de l’échantillon est donc
\[\begin{equation} \rho = \rho_w \frac{m}{m-m_a}. \end{equation}\]Cette méthode est plus précise que la méthode en vrac parce qu’on obtient le volume de l’échantillon en passant par une mesure de sa masse apparente dans l’eau. Cette mesure peut être faite avec une balance à haute précision et on n’a pas besoin de lire le volume d’eau déplacé sur un cylindre gradué. De plus, on peut corriger l’équation selon la densité de l’eau à la température du laboratoire. Dans les meilleures conditions, cette méthode offre des précisions allant jusqu’à 1 kg/m$^3$ (0.001 g/cm$^3$). Cependant, elle ne tient pas compte des micro porosités dans l’échantillon et le fait de submerger l’échantillon dans l’eau pourrait le détruire si celui-ci est faiblement consolidé. Selon le degré de saturation en eau de l’échantillon avant sa submersion, la densité obtenue par méthode d’Archimède est la densité apparente (échantillon non-saturé) ou la densité squelettique (échantillon dont les pores sont complètement remplis d’eau).
Méthode du pycnomètre
Les pycnomètres utilisent une cellule étanche contenant un gaz parfait (le plus souvent l’hélium) pour mesurer le volume d’un échantillon de géomatériau avec une meilleure précision que celui qui serait obtenu avec la méthode d’Archimède. Les pycnomètres sont équipés de deux cellules étanches, dont une peut accueillir l’échantillon. Le protocole de mesure est le suivant :
- Un échantillon, caractérisé par un volume $V$ et une masse $m$, est placé dans une cellule vide dont on connait le volume ($V_c$).
- Un volume connu de gaz est introduit dans la cellule et la pression initiale $P_i$ est mesurée.
- On ouvre la valve pour que le gaz s’étende vers une deuxième cellule de référence dont on connait le volume ($V_r$).
- La pression finale $P_f$ du système est mesurée.
Le volume de l’échantillon est ainsi donné par
\[\begin{equation*} V = V_r + V_c\left(1 - \frac{P_i}{P_f}\right), \end{equation*}\]et la densité est
\[\begin{equation*} \rho = m/V. \end{equation*}\]Cette méthode a comme avantage d’être applicable aux matériaux non-consolidés comme les sols, les poudres et même les liquides ou autres gaz. Cependant, la taille des cellules est relativement petite et les pycnomètres peuvent seulement accueillir des échantillons dont les dimensions sont de quelques centimètres.
Nucléodensimètre
Cette méthode est surtout utilisée pour obtenir des mesures de densité en forage. Une sonde est progressivement abaissée dans le trou de forage où une source radioactive (p. ex. le césium 137) émet des photons gamma qui vont interagir avec la paroi rocheuse par diffusion de Compton. Plus la roche est dense, plus les photons gamma seront diffusés. Un détecteur accompagne la sonde pour mesurer le phénomène de diffusion et ainsi obtenir la densité de la paroi du trou de forage. La profondeur d’investigation des nucléodensimètres est de quelques centimètres tout au plus.
Qu’est-ce qui détermine la densité d’une roche?
Porosité
Les espaces formés par la porosité des roches sont souvent remplis d’eau, de saumure, d’air, ou parfois même de gaz naturel ou de pétrole. Comme ces matériaux sont moins denses que leur hôte, la porosité peut contribuer à faire diminuer la densité apparente de la roche. Les effets de la porosité sur la densité des roches ne se font sentir que pour les roches dont la porosité est évidente (p. ex. les sédiments faiblement consolidés ou les roches volcaniques extrusives). À l’inverse, les roches intrusives et les sédiments archéens, par exemple, ont des porosités assez faibles, soit moins de 1%. Dans ce cas il est très difficile d’obtenir une mesure exacte de la densité squelettique d’un échantillon, mais on peut faire l’hypothèse qu’elle est comparable à sa densité apparente.
Composition géochimique
La composition géochimique détermine la densité squelettique de la plupart des roches peu poreuses.
Roches ignées : C’est principalement le ratio entre les éléments relativement légers (p. ex les minéraux à base de SiO$_2$) et les éléments plus lourds (p. ex. les minéraux riches en Fe) qui détermine la densité de la roche. En général, plus une roche ignée est felsique, moins elle est dense. À l’inverse, plus une roche est mafique, plus elle est dense.
Roches sédimentaires : La densité est déterminée par la composition géochimique de la roche. Cependant, il ne faut pas oublier que la composition des roches sédimentaires dépend de la source des grains qu’elle contient. De plus, les roches sédimentaires ont généralement été soumises à une forte pression hydrostatique, ce qui compacte les grains et réduit la porosité de la roche. Les roches sédimentaires qui ont subi une plus grande pression (comme celles au fond des bassins) ont tendance à être plus dense que celles qui sont moins compactées.
Roches métamorphiques : La densité découle non seulement du protolithe, mais elle est aussi affectée par l’historique des processus métamorphiques que la roche a subis.
Valeurs typiques de la densité
La partie supérieure de la croûte terrestre est caractérisée par une densité moyenne allant de 2690 à 2740 kg/m$^3$, alors que sa partie inférieure a une densité entre 3000 et 3250 kg/m$^3$. Le tableau suivant donne la densité de géomatériaux communs. Notez que les valeurs inférieures dans les gammes données se rapportent à des matériaux très meubles ou fortement aérés et que les matériaux géologiques peuvent avoir des densités très variables.
| Géomatériau | Densité (kg/m$^3$) |
|---|---|
| Argile (sèche) | 1600-2000 |
| Argile (saturée) | 2400 |
| Limon | 1700-2100 |
| Loam | 1360 |
| Sable | 1520 |
| Amphibolite | 2790-3140 |
| Dolomite | 2720-2840 |
| Gneiss | 2590-2840 |
| Calcaire (craie) | 1550-2200 |
| Calcaire (compact) | 2500-2750 |
| Marbre | 2670-2750 |
| Schiste | 2730-3190 |
| Shale | 2060-2670 |
| Ardoise | 2720-2840 |
| Pyrite | 5000 |
| Or | 19 300 |
Profil de densité de la Terre
La densité de la sous-surface varie grandement à l’échelle de la Terre. La Figure 2 montre le profil de densité de la Terre, de son coeur jusqu’à la croûte.
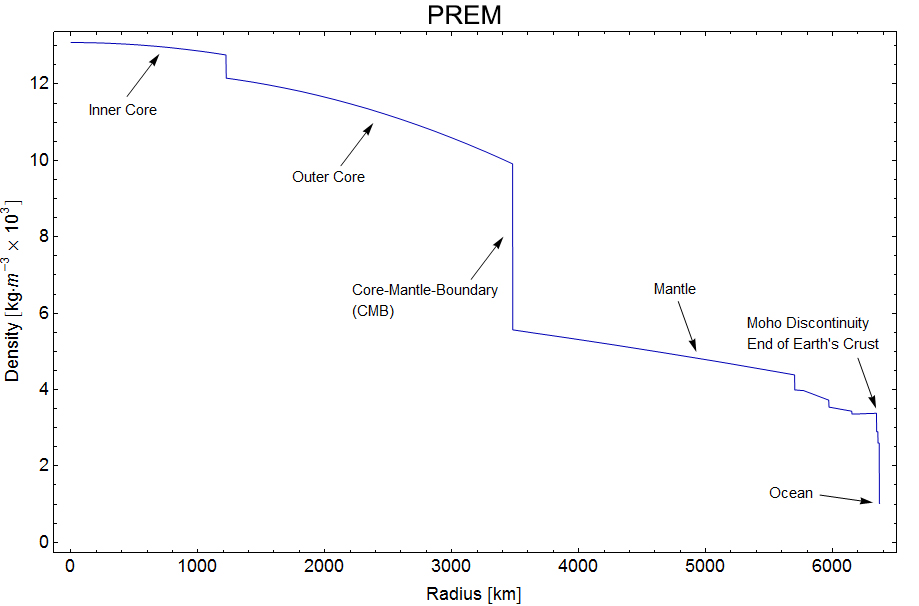
Figure 2. Profil de densité de la Terre. Source.
Pourriez-vous expliquer pourquoi la densité diminue progressivement du centre de la Terre vers la croûte?
Autres ressources
- Densité des types de roches et minéraux communs [anglais]
- Courte vidéo sur les mesures de densité avec la méthode d’Archimède [anglais]