2.1.5 Potentiel d’une sphère uniforme
- Modèle simplifié de la Terre
- Champ d’accélération gravitationnelle
- Potentiel gravitationnel
- Distribution radiale de la densité terrestre
Modèle simplifié de la Terre
Supposons que la Terre est une masse sphérique de rayon $R$ et dont la densité volumique de masse ($\rho$) est constante et uniforme dans le volume, tel que montré à la Figure 1.
Figure 1. Schéma montrant une sphère de Gauss ($S$) autour d’une sphère de rayon $R$ et de densité uniforme $\rho$.
Champ d’accélération gravitationnelle
On calcule le champ d’accélération gravitationnelle ($\boldsymbol{g}$) avec le théorème de Gauss, qui dit que
\[\iint_S \boldsymbol{g}\cdot \mathrm{d}\boldsymbol{S} = -4\pi G \iiint_V \rho\,\mathrm{d}V ,\]où $G$ est la constante gravitationnelle, $r$ est la distance à une surface de Gauss ($\boldsymbol{S} = S\ \boldsymbol{\hat{r}}$) et $V$ est le volume inclus dans $S$. De plus,
\[\mathrm{d}V = r'^2 \sin(\theta)\,\mathrm{d}\theta\,\mathrm{d}\phi\,\mathrm{d}r'\]et
\[\mathrm{d}S_r = r^2 \sin(\theta)\,\mathrm{d}\theta\,\mathrm{d}\phi\]dans un système de coordonnées sphériques.
Il faut séparer le problème en deux parties, car le champ à l’extérieur de la sphère n’est pas le même que celui à l’intérieur.
Pour $r \lt R$ :
\[\begin{align*} \iint_S \boldsymbol{g}\cdot \mathrm{d}\boldsymbol{S}_r & = -4\pi G \iiint_V \rho\,\mathrm{d}V \\ \int_0^{2\pi} \int_0^\pi (\boldsymbol{g}\cdot \boldsymbol{\hat{r}})\,r^2\sin{\theta}\,\mathrm{d}\theta\,\mathrm{d}\phi & = -4\pi G \int_0^r \int_0^{2\pi} \int_0^\pi \rho\ r'^2 \sin(\theta)\,\mathrm{d}\theta\,\mathrm{d}\phi\,\mathrm{d}r' \\ \boldsymbol{g}\cdot4\pi r^2\ \boldsymbol{\hat{r}} & = -4\pi G\rho \frac{4\pi r^3}{3} \\ -4\pi gr^2 & = -4\pi G\rho \frac{4\pi r^3}{3} \\ g & = \frac{4\pi G\rho}{3} r\ \\ \end{align*}\]Ce qui nous donne l’amplitude de $\boldsymbol{g}$. Cependant, on sait que le vecteur $\boldsymbol{g}$ pointe vers le centre de masse, donc dans la direction opposée à $\boldsymbol{\hat{r}}$. Alors pour écrire $\boldsymbol{g}$ en notation vectorielle on utilise
\[\boldsymbol{g} = -\frac{4\pi G\rho}{3} r\ \boldsymbol{\hat{r}},\]et comme on sait que $M = \rho V$ où $M$ est la masse de la Terre, alors
\[\boldsymbol{g} = -\frac{GM}{R^3} r\ \boldsymbol{\hat{r}}.\]Pour $r \gt R$ :
\[\begin{align*} \iint_S \boldsymbol{g}\cdot\mathrm{d}\boldsymbol{S}_r & = -4\pi G \iiint_V \rho\,\mathrm{d}V \\ \int_0^{2\pi} \int_0^\pi (\boldsymbol{g}\cdot \boldsymbol{\hat{r}})\,r^2\sin{\theta}\,\mathrm{d}\theta\,\mathrm{d}\phi & = -4\pi G \int_0^R \int_0^{2\pi} \int_0^\pi \rho\ r'^2 \sin(\theta)\,\mathrm{d}\theta\,\mathrm{d}\phi\,\mathrm{d}r' \\ \boldsymbol{g}\cdot4\pi r^2\ \boldsymbol{\hat{r}} & = -4\pi G\rho \frac{4\pi R^3}{3} \\ &\dots\\ \boldsymbol{g} & = -\frac{4\pi G\rho R^3}{3 r^2}\ \boldsymbol{\hat{r}} \\ \end{align*}\]Ce qui donne
\[\boldsymbol{g} = -\frac{GM}{r^2}\ \boldsymbol{\hat{r}}\]si on l’exprime en fonction de la masse de la Terre. On reconnait ici la loi universelle de l’attraction gravitationnelle. Quand on est à l’extérieur de la sphère c’est comme si sa masse était concentrée dans un point à l’origine.
On peut vérifier que $\boldsymbol{g}$ est continu à la surface de la sphère, à $\boldsymbol{g}(r = R)$. De plus, les cas limites sont $\boldsymbol{g}(r \to \infty) = 0$ et $\boldsymbol{g}(r \to 0) = 0$. Le champ d’accélération en fonction de la distance $r$ est montré à la Figure 2.
Figure 2. Champ gravitationnel ($g$) en fonction de la distance $r$ au centre d’une sphère uniforme de rayon $R$.
Le champ $\boldsymbol{g}$ dépend de $1/r^2$ à l’extérieur de la sphère, atteint un maximum à $r = R$ et diminue de façon linéaire à l’intérieur de la sphère, pour finalement atteindre 0 au centre.
Potentiel gravitationnel
On obtient le potentiel gravitationnel ($U$) en calculant le travail requis pour amener une masse unitaire ($m = 1$ kg) de l’infini au point $r$ dans le champ $\boldsymbol{g}$ :
\[U(r) = - \int_\infty^{r} \boldsymbol{g}(\boldsymbol{r'})\cdot\mathrm{d}\boldsymbol{r'}.\]Il faut résoudre cette intégrale dans les deux régions (extérieure et intérieure). Commençons par l’extérieur parce que la borne inférieure de l’intégrale est $\infty$.
Pour $r \gt R$ :
\[\begin{align*} U(r) & = - \int_\infty^{r} \boldsymbol{g}(\boldsymbol{r'})\cdot\mathrm{d}\boldsymbol{r'} \\ & = - \int_\infty^{r} - \frac{GM}{r'^2}\,\mathrm{d}r' \\ & = - GM \left[ \frac{1}{r'} \right]_\infty^r. \\ \end{align*}\]On trouve que le potentiel à l’extérieur de la sphère est :
\[\begin{equation} U(r) = - \frac{GM}{r}. \\ \end{equation}\]Notez le cas limite $U(r\to\infty) = 0$.
On peut aussi vérifier que le potentiel à l’extérieur de la sphère uniforme respecte l’équation de Laplace. L’opérateur laplacien en coordonnées sphériques est :
\[\nabla^2 U= \frac{1}{r^2}\frac{\partial}{\partial r}\left( r^2 \frac{\partial U}{\partial r} \right) + \frac{1}{r^2 \sin\theta}\frac{\partial}{\partial \theta}\left( \sin\theta \frac{\partial U}{\partial \theta} \right) + \frac{1}{r^2 \sin^2\theta}\frac{\partial^2 U}{\partial \phi^2} .\]Notez qu’à cause de la symétrie sphérique les deux termes à droites sont nuls, car le potentiel ne dépend pas de la colatitude ($\theta$) ni de l’azimut ($\phi$). On trouve
\[\nabla^2 U = 0 .\]Pour $r \lt R$ :
À l’intérieur de la sphère uniforme, le potentiel est donné par le potentiel à la surface plus le potentiel obtenu avec le travail requis pour déplacer une masse unitaire de $R$ à $r$, où $r \lt R$.
\[\begin{align*} U(r) & = U(R) - \int_R^{r} \boldsymbol{g}(\boldsymbol{r'})\cdot\mathrm{d}\boldsymbol{r'} \\ & = U(R) - \int_R^{r} -\frac{GM}{R^3} r'\,\mathrm{d}r' \\ & = U(R) + \frac{GM}{R^3} \left[ \frac{r'^2}{2}\right]_R^r \\ & = U(R) + \frac{GM}{2R^3} \left[ r^2 - R^2 \right]. \\ \end{align*}\]On se souvient que le potentiel à la surface est donné par l’équation (8) évaluée à $r=R$ :
\[\begin{equation} U(R) = - \frac{GM}{R} , \end{equation}\]donc
\[\begin{align*} U(r) & = - \frac{GM}{R} + \frac{GM}{2R^3} \left[ r^2 - R^2 \right] \\ & = - \frac{GM}{R} + \frac{GMr^2}{2R^3} - \frac{GM}{2R} \\ & = - \frac{2GMR^2}{2R^3} + \frac{GMr^2}{2R^3} - \frac{GMR^2}{2R^3} .\\ \end{align*}\]On trouve finalement que
\[\begin{equation} U(r) = -\frac{GM}{2R^3} \left( 3R^2 - r^2 \right). \end{equation}\]Notez le cas limite $U(r\to 0) = -\frac{3GM}{2R}$, qui dit que le potentiel est une constante au centre de la sphère. Notez aussi que le potentiel est continu à $r = R$.
On peut vérifier que le potentiel à l’intérieur de la sphère uniforme respecte l’équation de Poisson :
\[\begin{align*} \nabla^2 U & = \frac{1}{r^2}\frac{\partial}{\partial r}\left( r^2 \frac{\partial U}{\partial r} \right) \\ & = \frac{1}{r^2}\frac{\partial}{\partial r}\left( r^3 \frac{GM}{R^3} \right) \\ & = \frac{3GM}{R^3} \\ & = \frac{3G}{R^3} \frac{4\pi R^3}{3} \rho \\ \end{align*}\]On retrouve comme prévu que
\[\begin{equation} \nabla^2 U= 4\pi G \rho . \end{equation}\]Distribution radiale de la densité terrestre
En réalité on sait que la densité de la Terre n’est pas uniforme et qu’elle varie selon la distance où on se trouve par rapport à son centre, tel que montré à la Figure 3.
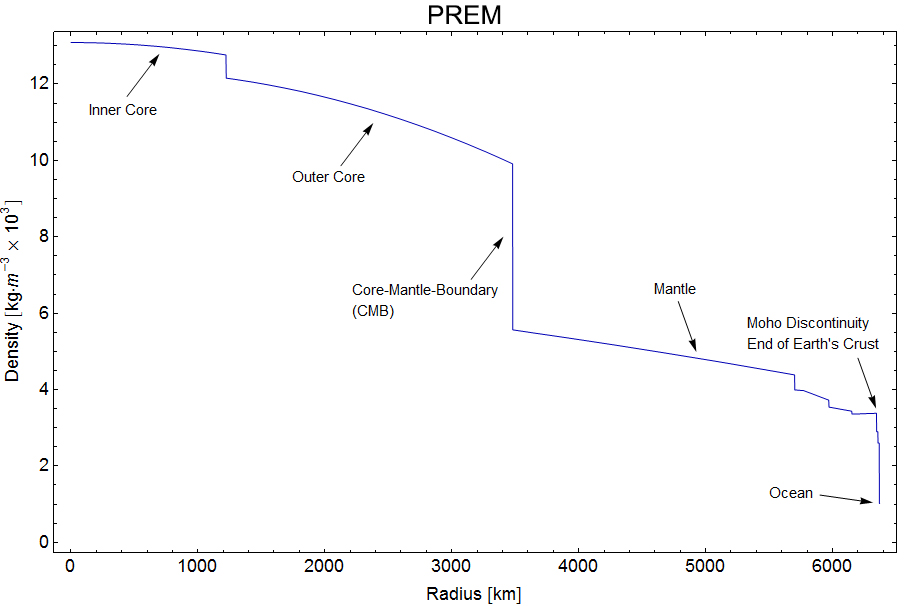
Figure 3. Profil de la densité radiale de la Terre. Source.
On sait que la densité de la Terre près de son centre est d’environ 13 000 kg/m$^3$ et que la densité diminue pour atteindre 2800 kg/m$^3$ au niveau de la croûte terrestre. On pourrait, pour améliorer notre approximation, supposer que la densité varie linéairement avec le rayon selon la relation
\[\rho(r') = a - br' ,\]où $a$ et $b$ sont des constantes propres à une planète. Dans le cas de la Terre, on pourrait dire que $a \approx 1.3\times 10^4$ kg/m$^3$, $b \approx 1.6\times 10^{-3}$ kg/m$^4$ et $R \approx 6.371\times 10^6$ m.
Vous utiliserez cette approximation dans le Devoir 2 pour montrer que le potentiel gravitationnel de la Terre obéit à l’équation de Poisson même si la densité varie radialement.