2.4.7 Exemples
Plusieurs types de formations géologiques peuvent être paramétrisées par des géométries simples. Cette section donne quelques exemples.
Tube de lave
Les tubes de lave se forment lorsque des coulées de lave refroidissent et durcissent en surface, formant une coquille au-dessus de coulées de laves encore chaudes (Figure 1). Ces coulées peuvent laisser des cavités dans la lave après son refroidissement complet.

Figure 1. Exemple d’un tube de lave. Source : USGS.
Un tube de lave crée donc un contraste de densité négatif avec la roche encaissante. On peut paramétriser un tube de lave comme un cylindre dont le pendage est $\alpha$, l’aire de la section est $A$ et la longueur est $L$ (Figure 2).
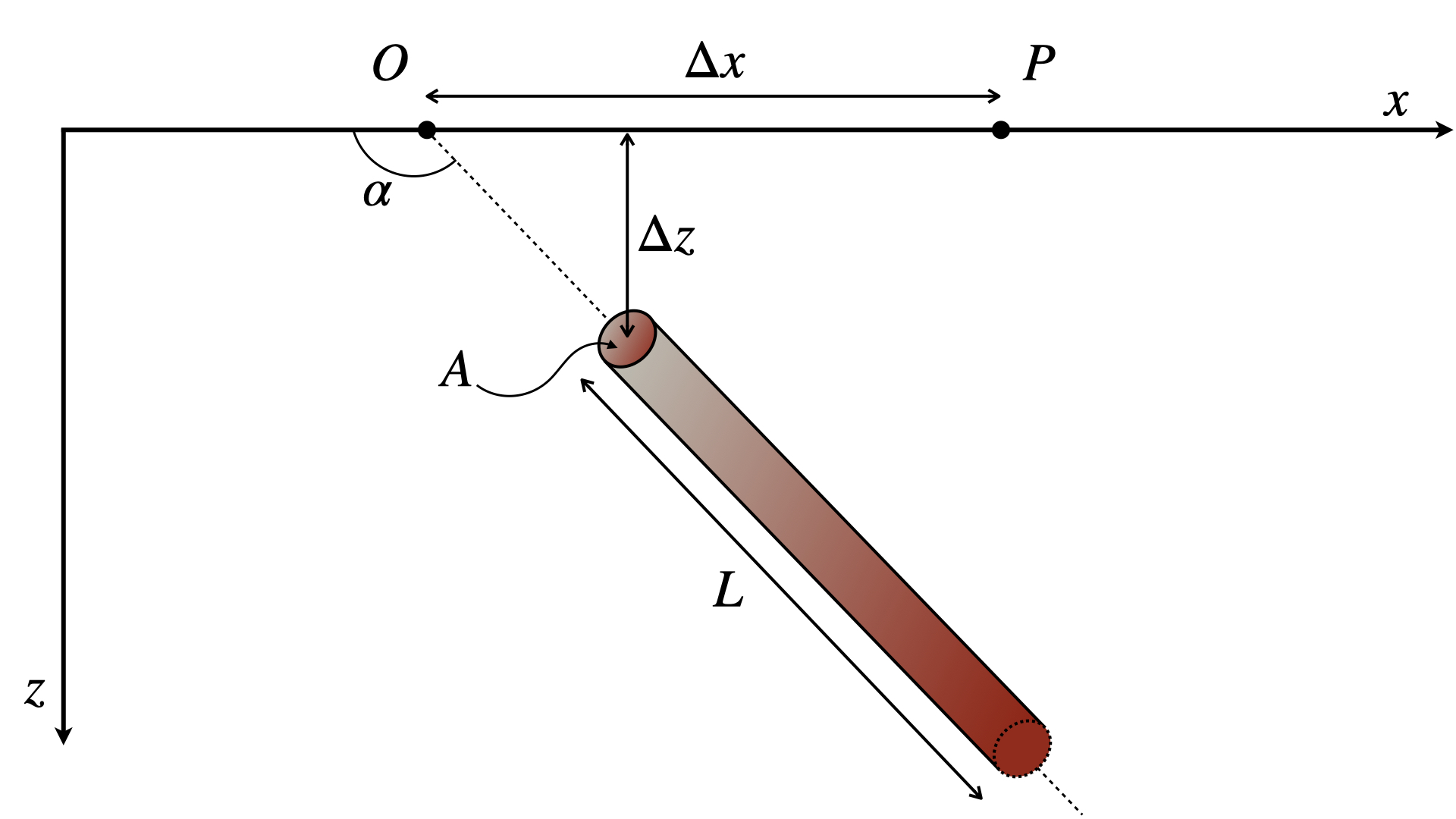
Figure 2. Schéma montrant une façon de paramétriser un tube de lave.
Si on suppose que le rayon du cylindre est beaucoup plus petit que sa longueur, la composante verticale de l’anomalie gravimétrique $\Delta g_z$ du cylindre est [1] :
\[\begin{split} \Delta g_z &= \frac{GA\Delta\rho }{\Delta x\sin\alpha} \Biggl\{\frac{\Delta x + \Delta z\cot\alpha}{\left[\Delta z^2 \csc^2 \alpha +2\Delta x\Delta z\cot\alpha +\Delta x^2\right]^{1/2}} - \\ &\quad \frac{\Delta x + \Delta z\cot\alpha + L\cos\alpha}{\left[(L + \Delta z\csc\alpha)^2 + \Delta x^2 + 2\Delta x(L\cos\alpha + \Delta z\cot\alpha)\right]^{1/2}} \Biggr\}, \end{split}\]où
- $\Delta z = z_0 - z$
- $\Delta x = x - (x_0 + \Delta z \cot\alpha)$
représentent les distances identifiées sur la Figure 2 et $G$ est la constante gravitationnelle.
Tube vertical infini
Notez que quand $\alpha = 90^{\circ}$, alors $\sin\alpha = 1$, $\cos\alpha=0$, $\cot\alpha = 0$ et $\csc\alpha = 1$. L’équation se simplifie donc à
\[\Delta g_z = GA\Delta\rho \left\{\frac{1}{(\Delta z^2 + \Delta x^2)^{1/2}} - \frac{1}{\left[(L + \Delta z)^2 + \Delta x^2 \right]^{1/2}} \right\} .\]Et si $L \to \infty$, alors
\[\Delta g_z = GA\Delta\rho \left[\frac{1}{(\Delta z^2 + \Delta x^2)^{1/2}} \right] .\]Sensibilité au pendage
La Figure 3 montre l’effet du pendange ($\alpha$) sur la réponse gravimétrique du cylindre. Les variables utilisées pour la simulation sont $x_0 = 50$ m, $z_0 = 10$ m, $A = \pi\times 10^2$ m$^2$, $L = 100$ m et $\Delta\rho = -3000$ kg/m$^3$.
Figure 3. Effet du pendage du tube de lave sur sa réponse gravimétrique.
Faille normale
Supposons qu’une faille normale crée un déplacement vertical dans une unité de dolérite (Figure 4). L’unité de dolérite a une densité (3000 kg/m$^3$) qui est supérieure à celle de la roche sédimentaire (2600 kg/m$^3$).
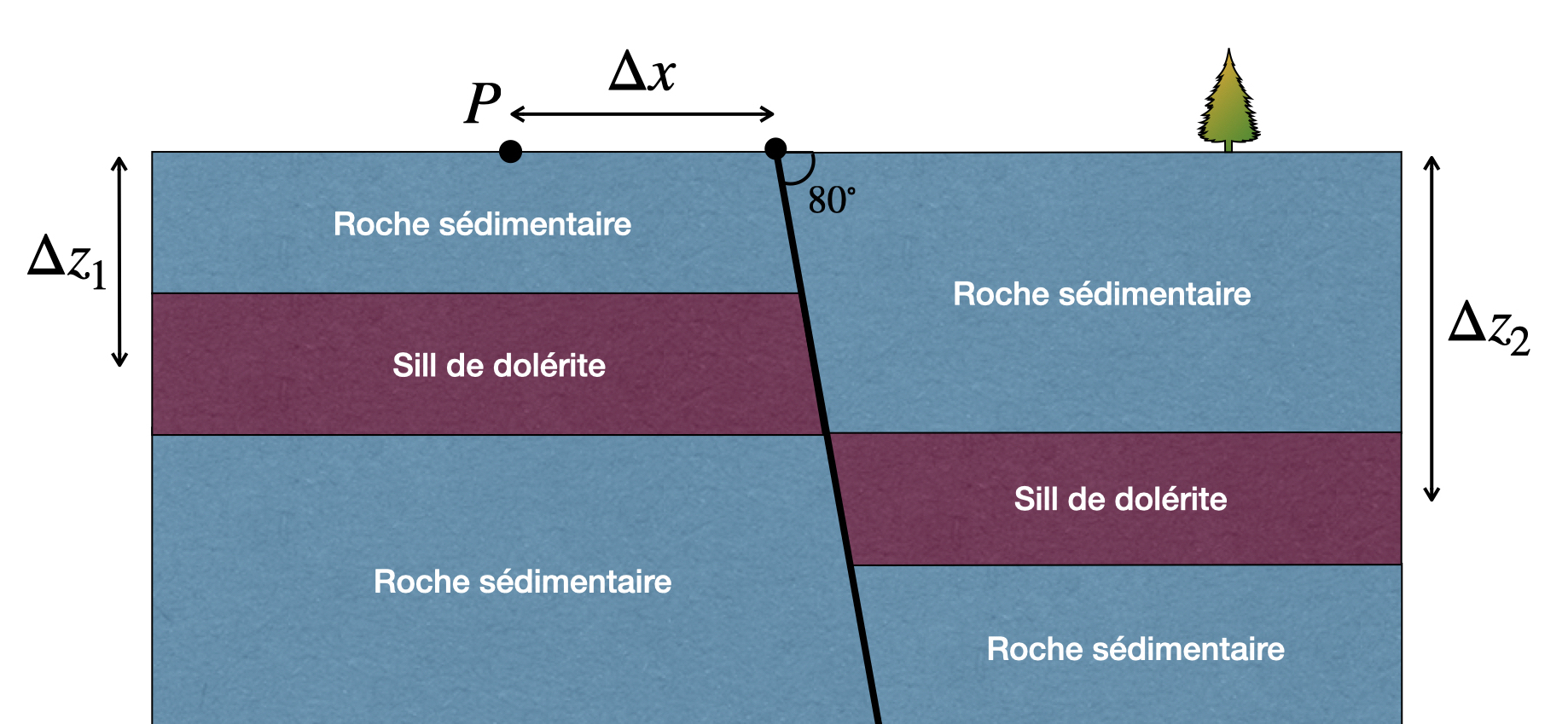
Figure 4. Schéma d’une faille normale.
On peut approximer ce modèle comme la superposition de deux plaques minces semi infinies qui créent un contraste de densité $\Delta\rho = +1000$ kg/m$^3$ avec leur milieu encaissant. Si $t$ est l’épaisseur du sill, alors la réponse gravimétrique de la faille est
\[\begin{equation} \Delta g_z = 2Gt\Delta\rho \left[ \pi + \tan^{-1}\left(\frac{\Delta x}{\Delta z_2}\right) - \tan^{-1}\left(\frac{\Delta x}{\Delta z_1}\right) \right] , \end{equation}\]où les distances $\Delta x$, $\Delta z_1$ et $\Delta z_2$ sont identifiées sur la Figure 4.
Références
- Telford, W. M., Geldart, L. P., & Sheriff, R. E. (1990). Applied Geophysics. Cambridge : Cambridge University Press.