4.2.5 Principe de mesure
- Aimantation des sources géologiques
- Mesure du champ magnétique total
- Instruments de mesures
- Traitement des données magnétiques
- Références
Aimantation des sources géologiques
Avant de décrire mathématiquement les anomalies que la méthode magnétique vise à caractériser, il faut illustrer de façon intuitive ce qui se passe quand une unité géologique, qui présente un contraste de susceptibilité magnétique avec son milieu encaissant, baigne dans le champ magnétique de la Terre. La Figure 1 montre une formation géologique de susceptibilité magnétique $\chi_m$ enfouie dans un milieu encaissant non magnétique.
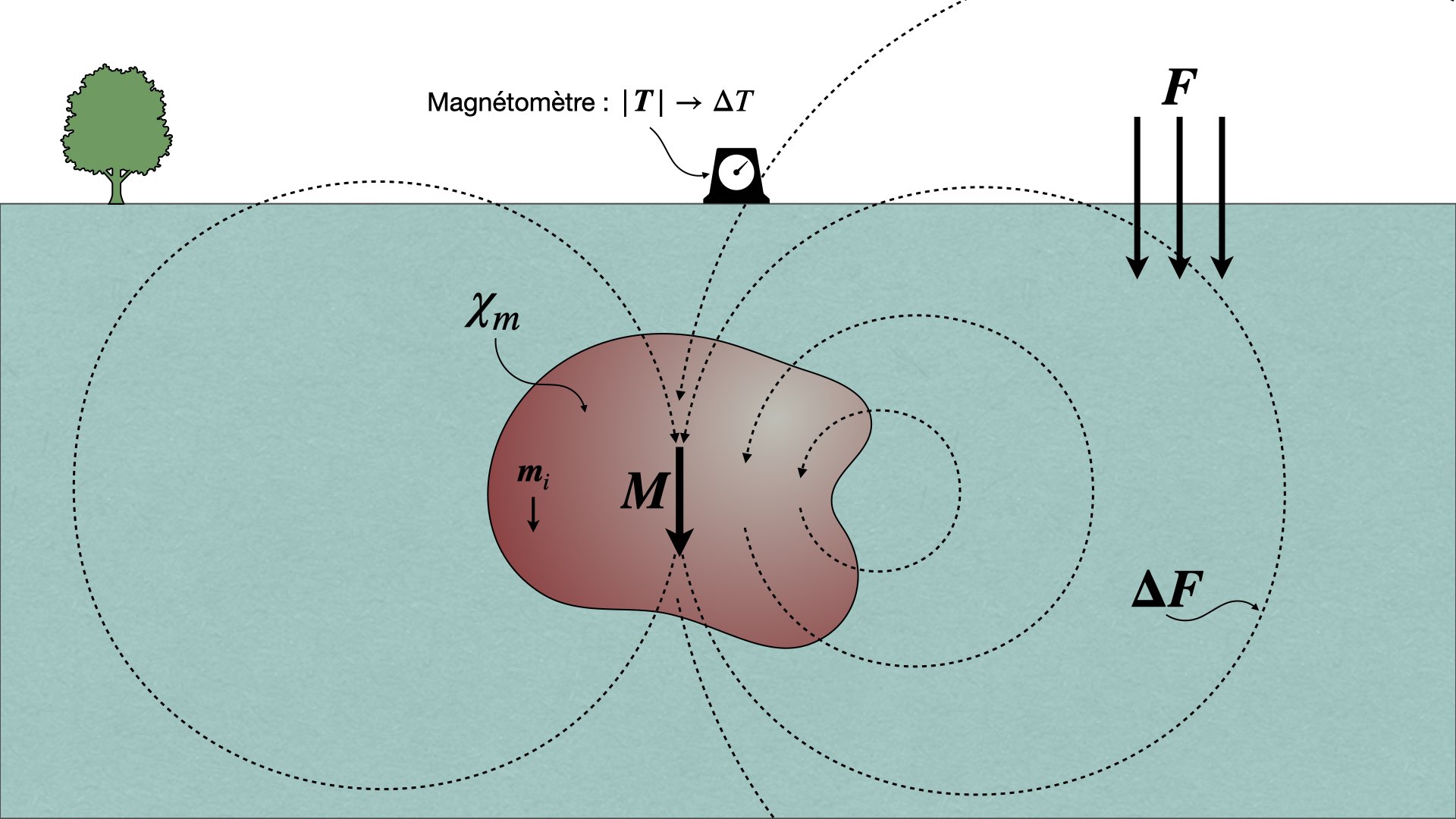
Figure 1. Principe de la méthode magnétique.
Le champ régional, qu’on appelle aussi champ primaire, est dénoté par $\boldsymbol{F}$ dans la Figure 1. C’est celui qui est décrit par l’IGRF, par exemple.
Comme l’unité géologique a une susceptibilité magnétique non nulle et qu’elle baigne dans $\boldsymbol{F}$, il se crée une aimantation induite dans celle-ci ($\boldsymbol{M}$). Il est important de noter que $\boldsymbol{M}$ est induite dans la même direction que $\boldsymbol{F}$.
Cette aimantation induite se traduit par un moment dipolaire ($\boldsymbol{m}$) dans l’unité géologique. Ce moment dipolaire crée à son tour un champ magnétique ($\boldsymbol{\Delta F}$), qu’on appelle le champ secondaire. $\boldsymbol{\Delta F}$ forme des boucles qui tournent autour du moment dipolaire de l’aimantation induite et déforme légèrement le champ primaire : c’est une anomalie dans le champ régional.
Un magnétomètre est placé à la surface terrestre, dans un avion ou dans un bateau pour mesurer l’amplitude du champ total ($\boldsymbol{T}$ est le vecteur du champ total et $T$ est son amplitude). Finalement, les spécialistes en géophysique calculent l’anomalie du champ total ($\Delta T$) pour interpréter la réponse de l’unité géologique. Notez comment les lignes de champ de $\boldsymbol{\Delta F}$ passent dans le magnétomètre avec un angle différent que celui de $\boldsymbol{F}$.
Mesure du champ magnétique total
La méthode magnétique (ou magnétométrie) en géophysique appliquée emploie des «magnétomètres à champ total» pour mesurer l’amplitude du champ magnétique. C’est là une première différence avec la méthode de gravimétrie, où l’on mesurait seulement la composante verticale de la gravité. Avec la méthode magnétique, on s’intéresse à toutes les composantes du champ en mesurant l’intensité totale (la norme du vecteur), sans trop se préoccuper de sa direction.
De plus, les magnétomètres mesurent la valeur absolue du champ magnétique observé. C’est la deuxième différence avec la méthode de gravimétrie, où l’on utilisait des gravimètres relatifs pour caractériser les anomalies. Tel que mentionné dans la section précédente, on obtient le champ magnétique créé par les anomalies géologiques dans la croûte en soustrayant un modèle régional (p. ex. celui de l’IGRF) au champ total mesuré.
Anomalie du champ total
Si $\boldsymbol{T}$ est le champ magnétique total (celui qui sera mesuré par le magnétomètre) et $\boldsymbol{F}$ est un champ magnétique régional uniforme, alors
\[\Delta T = \vert\boldsymbol{T}\vert - \vert\boldsymbol{F}\vert\]est l’anomalie du champ magnétique total. Notez bien que $\Delta T$ est une valeur scalaire. Supposons maintenant qu’il existe une anomalie dans le champ régional ($\boldsymbol{\Delta F}$).
⚠️ Attention, $\boldsymbol{\Delta F}$ n’est pas uniforme et ne pointe pas nécessairement dans la même direction que le champ régional. $\boldsymbol{\Delta F}$ correspond au champ secondaire que génèrerait une anomalie géologique qui viendrait perturber le champ régional. Ça pourrait être, par exemple, une intrusion de roche ignée qui a une forte aimantation à cause de son contenu en magnétite.
À cause de l’anomalie $\boldsymbol{\Delta F}$, le champ total serait maintenant :
\[\boldsymbol{T} = \boldsymbol{F} + \boldsymbol{\Delta F} ,\]ce qui donne une nouvelle anomalie du champ total égale à
\[\Delta T = \vert\boldsymbol{\boldsymbol{F} + \boldsymbol{\Delta F}}\vert - \vert\boldsymbol{F}\vert\]Anomalies magnétiques anticipées
Les anomalies causées par les contrastes de susceptibilité magnétique dans la croûte ($\boldsymbol{\Delta F}$) sont généralement de l’ordre de 1 nT à 1000 nT. Celles-ci dépassent très rarement 5000 nT, sauf pour des objets métalliques enfouis près de la surface. Comme on l’a vu précédemment, l’intensité du champ magnétique régional ($\boldsymbol{F}$) au Canada est d’environ 55 000 nT. On peut donc faire l’approximation que, dans les applications de la méthode magnétique en géophysique, $\boldsymbol{\Delta F} \ll \boldsymbol{F}$.
L’équation (3) s’approxime par
\[\begin{align*} \Delta T &= \vert\boldsymbol{F} + \boldsymbol{\Delta F}\vert - \vert\boldsymbol{F}\vert,\\ &= (\boldsymbol{F}\cdot\boldsymbol{F} +2\boldsymbol{F}\cdot\boldsymbol{\Delta F} + \boldsymbol{\Delta F}\cdot\boldsymbol{\Delta F})^{1/2} - \vert\boldsymbol{F}\vert,\\ &\approx (\boldsymbol{F}\cdot\boldsymbol{F} +2\boldsymbol{F}\cdot\boldsymbol{\Delta F})^{1/2}- \vert\boldsymbol{F}\vert,\\ &\approx \frac{\boldsymbol{F}\cdot\boldsymbol{\Delta F}}{\vert\boldsymbol{F}\vert},\\ \end{align*}\]On trouve finalement que l’anomalie du champ total est
\[\Delta T \approx \boldsymbol{\hat{F}} \cdot \boldsymbol{\Delta F} ,\]ce qui correspond à la projection de l’anomalie régionale sur le champ régional. Au final, ça veut dire que dans cette approximation où les anomalies anticipées sont beaucoup plus faibles que le champ régional, l’anomalie du champ total est approximativement égale à la projection de l’anomalie régionale sur le champ régional (Figure 2).
⚠️ Vous devriez maintenant avoir réalisé que $\Delta T$ est l’analogue de $\Delta g_z$ : l’anomalie que l’on cherchait en gravimétrie.
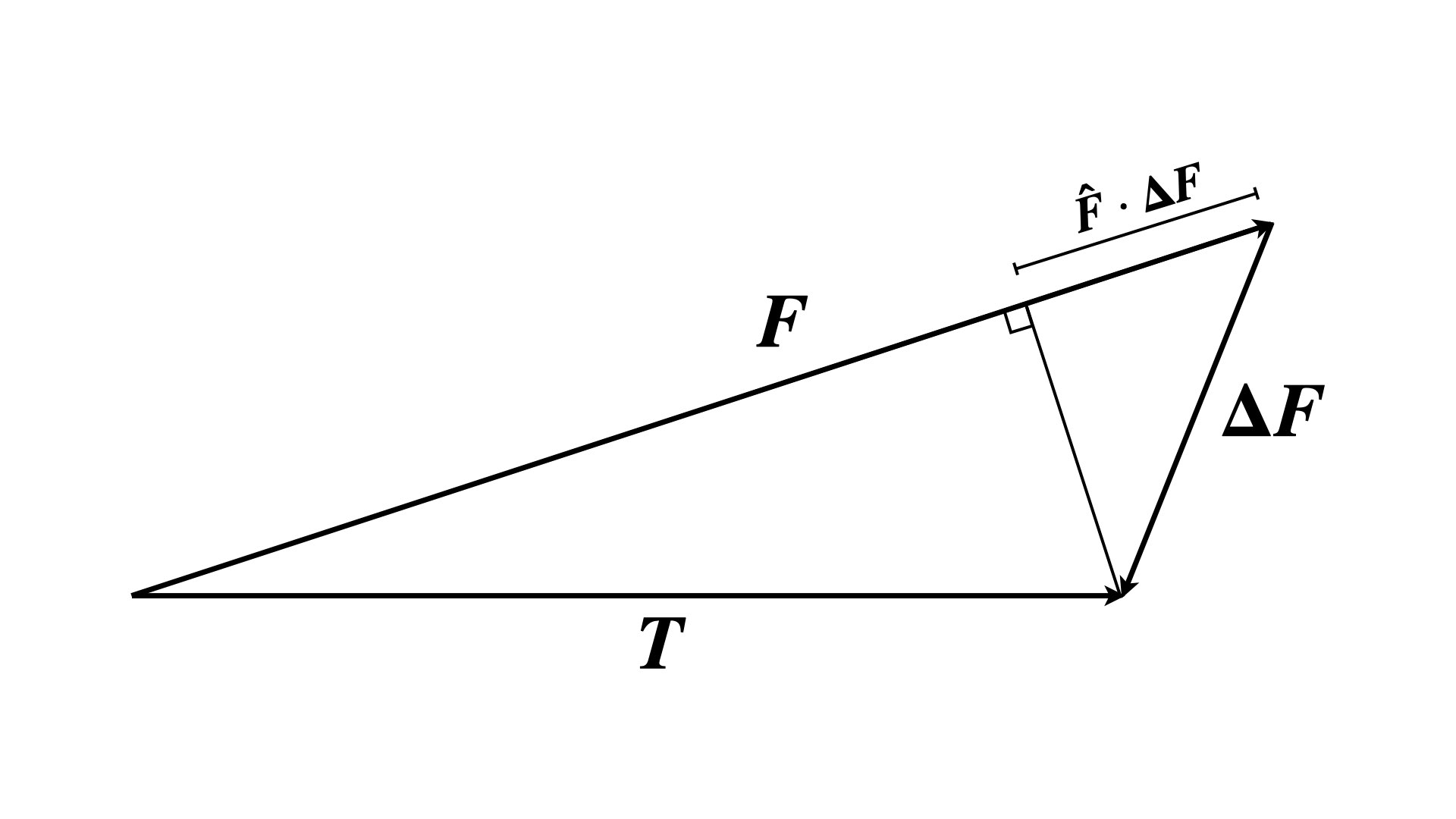
Figure 2. Représentation vectorielle des anomalies de champ total.
Équation de Laplace
Il serait intéressant de vérifier que l’anomalie de champ total ($\Delta T$) respecte l’équation de Laplace. Ça voudrait dire que c’est une fonction harmonique et qu’on pourrait utiliser toutes les notions d’analyse spectrale qu’on a vu au chapitre 3, comme le filtrage par prolongement vers le haut, le processus de séparation régionale-résiduelle, et le calcul du gradient spatial et/ou du signal analytique, entre autres. En appliquant l’opérateur laplacien à l’équation (4) on obtient
\[\nabla^2 \Delta T = \nabla^2 (\boldsymbol{\hat{F}} \cdot \boldsymbol{\Delta F})\]et si le levé magnétique se fait à relativement petite échelle et que $\Delta F$ peut conséquemment être considéré comme un champ uniforme (une constante), alors on peut le sortir du laplacien
\[\nabla^2 \Delta T = \boldsymbol{\hat{F}} \cdot \nabla^2 (\boldsymbol{\Delta F}) .\]Comme $\boldsymbol{\Delta F}$ peut être exprimé comme une expansion en harmoniques sphériques, son laplacien est automatiquement égal à 0 et on trouve
\[\nabla^2 \Delta T = 0 .\]On en déduit finalement que l’anomalie de champ total est une fonction harmonique et se comporte comme un potentiel, tant que le champ primaire régional puisse être considéré uniforme sur la surface du levé.
Instruments de mesures
Il est recommandé de lire la section 3.5 de Reynolds disponible sur le site Moodle du cours. Cette section porte exclusivement sur le fonctionnement des différents types de magnétomètres et systèmes de mesure.
Traitement des données magnétiques
On ne traite pas les données magnétiques de la même façon qu’on traite les données gravimétriques. Alors qu’on avait établi des façons de corriger les données pour retirer les effets de la dérive, de l’altitude, de la latitude, du plateau du relief, ces corrections ne s’appliquent généralement pas à la méthode magnétique.
En effet, comme on le verra dans la prochaine section, une tranche de Bouguer uniformément aimantée n’a même pas de réponse magnétique, il n’est donc pas nécessaire d’appliquer cette correction. De plus, on va automatiquement tenir compte de l’influence de la latitude et de la variation séculaire à long terme quand on rapporte les données magnétiques au niveau de l’IGRF.
Pour ce qui est de la variation séculaire diurne (à court terme) on va souvent employer la même stratégie qu’en gravimétrie, c’est-à-dire qu’on va effectuer une correction de dérive d’après les mesures obtenues à une station de base tout au long de la journée.
Finalement, il nous reste l’altitude du levé et le relief, qui sont deux facteurs avec des impacts considérables sur les données magnétiques. Cependant, la correction pour ces effets est de nature numérique et emploie des algorithmes qui peuvent être assez complexes. On choisit habituellement de corriger ces effets au stade de la modélisation numérique et de l’interprétation, puisqu’il est possible de paramétriser la géologie et l’altitude du levé dans un modèle discrétisé en 2D ou 3D.
Pour reprendre les mots de [1], on traite les données magnétiques de façon beaucoup plus «cavalière».
Références
- Blakely, R. J. (1995). « The Geomagnetic Field », dans Potential Theory in Gravity and Magnetic Applications, Cambridge: Cambridge University Press, p. 154–181.