4.2.1 Champ magnétique terrestre
- La méthode magnétique
- Description du champ géomagnétique
- Cartes isomagnétiques 2020–2025
- Autres ressources
La méthode magnétique
Le géomagnétisme est l’étude du champ magnétique de la Terre. La méthode magnétique (ou magnétométrie) en géophysique permet d’étudier les contrastes de susceptibilité magnétique dans le sol (Chapitre 1). Avec les instruments actuels, la mesure du champ magnétique terrestre peut se faire à des fréquences temporelles très élévées (plusieurs mesures par seconde), ce qui ouvre la porte à la réalisation de levés magnétiques aéroportés, par exemple par drone, hélicoptère ou avion, pour couvrir des surfaces immenses de la surface terrestre, et ce à très haute résolution. La méthode magnétique est une autre méthode géophysique dite « de potentiel » (ou linéaire), comme la gravimétrie. La modélisation directe et inverse pour interpréter les données magnétiques est donc relativement simple.
Parallèle avec la gravité
Dans le chapitre sur la gravimétrie, on a décrit les sources qui influencent l’accélération gravitationnelle à la surface terrestre. Notre but était d’identifier toutes les sources qui ne sont pas attribuables à des contrastes de densité dans le sol, pour retirer leur effets et ainsi obtenir l’anomalie de Bouguer. Finalement, l’analyse de l’anomalie de Bouguer nous a permis de modéliser les contrastes de densité dans le sol. On fera un cheminement semblable en magnétisme, sauf que le champ magnétique de la Terre est beaucoup plus complexe que son champ de gravité. Notamment, le champ géomagnétique
- n’est pas uniquement radial,
- varie considérablement dans le temps,
- est influencé par des sources internes et externes.
Avant d’aller plus loin dans notre étude du champ magnétique pour cartographier les contrastes de susceptibilité magnétique dans la géologie, il faut s’arrêter un instant pour comprendre comment les particularités du champ géomagnétique peuvent être prédites. Il est aussi recommandé de relire la section sur l’aimantation et la susceptibilité magnétique dans le Chapitre 1.
Description du champ géomagnétique
Composantes vectorielles
Comme on l’a vu dans la section 4.1, le champ magnétique est une quantité vectorielle. De façon générale, un champ magnétique est défini comme le vecteur $\boldsymbol{B} = B\ \boldsymbol{\hat{b}}$, où $\boldsymbol{\hat{b}}$ est le vecteur unitaire qui donne sa direction.
En géomagnétisme, on va souvent l’exprimer comme son intensité totale ($F$), son inclinaison ($I$) et sa déclinaison ($D$). Ça revient en quelque sorte à exprimer le champ en coordonnées sphériques.
La déclinaison du champ est définie comme l’angle que fait un méridien magnétique par rapport au nord géographique (l’azimuth du méridien magnétique). C’est donc l’angle horizontal entre les lignes de champ et les lignes de longitudes, défini comme positif vers l’Est.
L’inclinaison du champ représente l’angle vertical que celui-ci fait par rapport à la surface terrestre. L’inclinaison est définie comme positive sous la surface terrestre Un méridien magnétique correspond à un plan vertical qui relie les pôles Sud et Nord magnétiques. Les angles d’inclinaison et de déclinaison sont montrés à la Figure 1.
Pour un observateur qui se situe à un endroit sur la surface terrestre, il est commun de rapporter ces notions dans un système de coordonnées cartésiennes. Par convention, on utilise l’axe des $x$ comme étant l’axe qui pointe ver le Nord géographique et on utilise l’axe des $y$ comme étant l’axe qui pointe vers l’Est géographique. L’axe des $z$ pointe vers l’intérieur de la Terre (Figure 1). On a donc que
\[\boldsymbol{B} = B_x\ \boldsymbol{\hat{x}} + B_y\ \boldsymbol{\hat{y}} + B_z\ \boldsymbol{\hat{z}},\]Convention
Pour simplifier la notation, une convention a été adoptée pour désigner les différentes composantes du champ géomagnétique. Ainsi, la Commission géologique du Canada, le British Geological Survey et le USGS utilisent la même notation. Il en découle que les différentes composantes du champ géomagnétique sont reliées par les quantités scalaires suivantes :
\[F = \sqrt{B_x^2 + B_y^2 + B_z^2} \qquad \text{(l'intensité totale)} ,\] \[H = \sqrt{B_x^2 + B_y^2} \qquad \textrm{(l'intensité horizontale)} ,\] \[I = \arctan{\frac{B_z}{\sqrt{B_x^2 + B_y^2}}} \qquad \text{(l'inclinaison)} ,\] \[D = \arctan2{(B_y, B_x)} \qquad \text{(la déclinaison)} .\]Plusieurs livres de référence simplifient la notation des trois composantes avec :
\[\begin{align} X &= B_x \\ Y &= B_y \\ Z &= B_z. \end{align}\]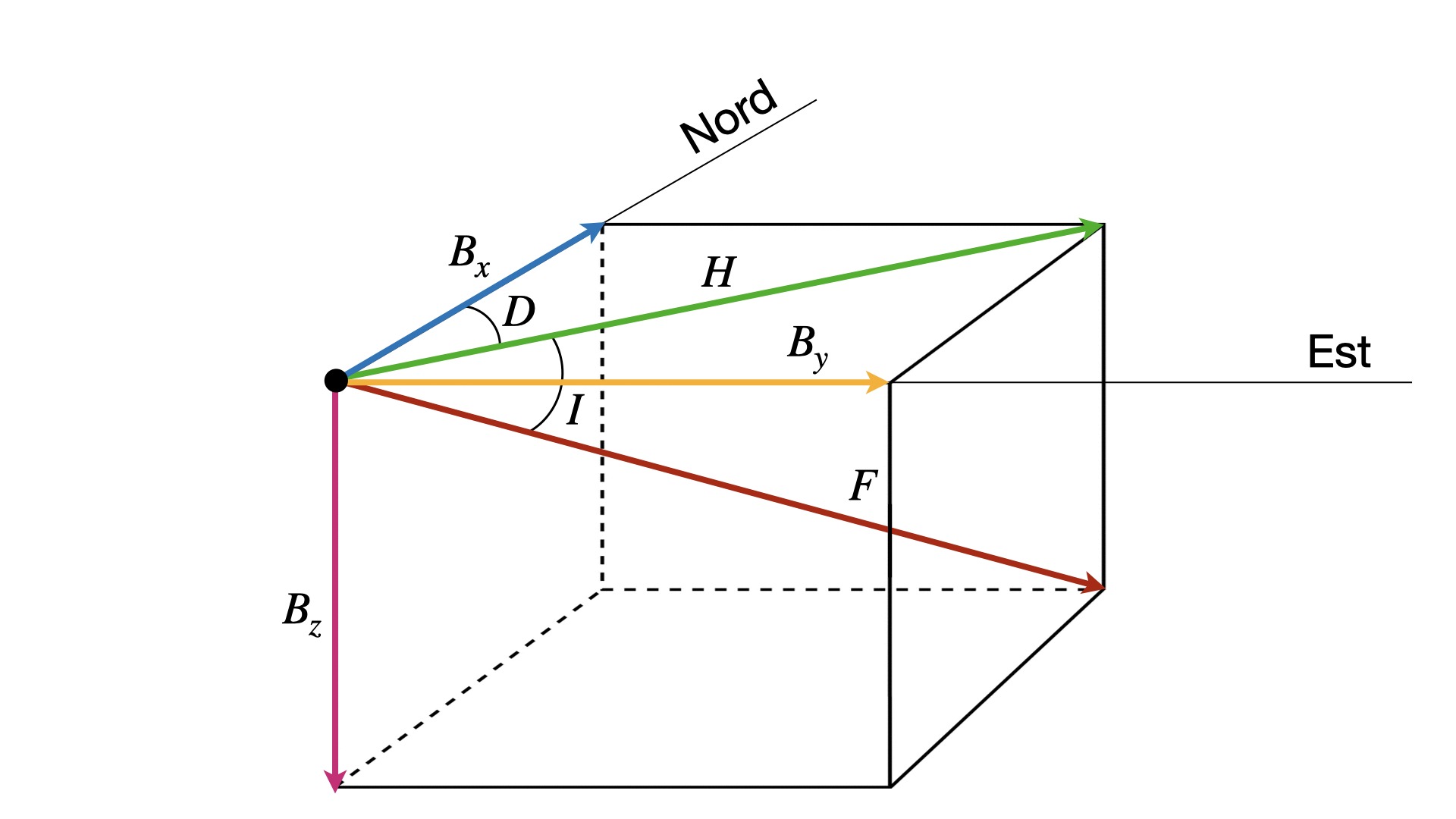
Figure 1. Représentation géométrique des composantes du champ magnétique.
Modélisation à différentes échelles
À l’échelle humaine des applications géophysiques (plusieurs centaines de kilomètres), le champ magnétique peut être approximé comme un champ uniforme, c’est-à-dire que sa norme et sa direction sont constantes et ne dépendent pas de la position où on se trouve. Il devient assez facile de le paramétriser dans ce cas (Figure 2). Le gradient moyen du champ magnétique étant d’environ 5 à 20 nT par 100 km, cette hypothèse est utile en prospection locale, mais reste une approximation à l’échelle régionale.
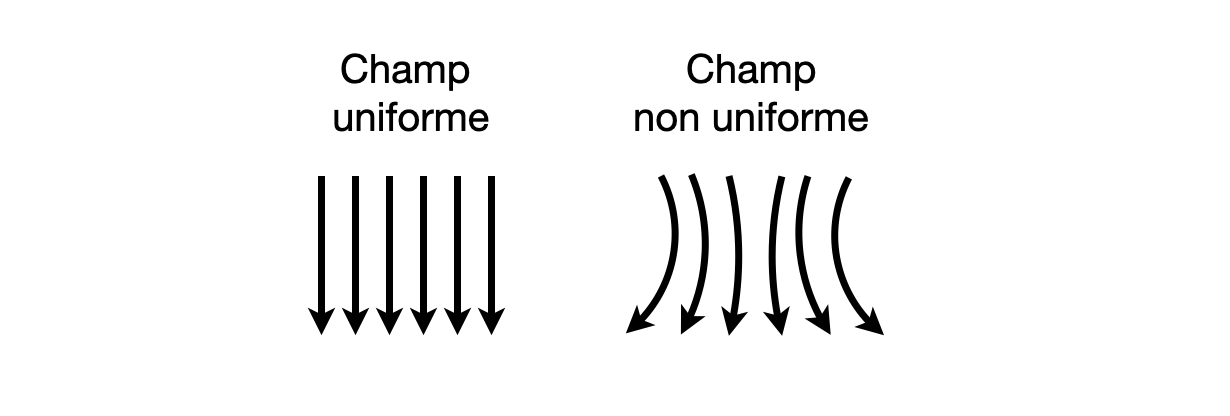
Figure 2. Comparaison entre un champ uniforme et un champ non uniforme.
Cependant, à l’échelle des continents et à l’échelle du globe, le champ géomagnétique doit être modélisé plus précisément pour tenir compte des variations spatiales de ses différentes composantes. L’équation qui décrit le potentiel du champ magnétique de la Terre est obtenue par analyse des harmoniques sphériques (Figure 3). Le potentiel à la surface de la Terre est :
\[V = a\sum_{n=1}^{\infty} \left[\left(\frac{r}{a}\right)^n T_n^e + \left(\frac{a}{r}\right)^{n+1} T_n^i \right] ,\]où $r$ est la distance à laquelle on veut calculer le potentiel (à partir du centre de la Terre) et $a$ est le rayon moyen de la Terre. $T_n^e$ et $T_n^i$ sont respectivement des termes qui décrivent les contributions des sources internes ($i$) et externes ($e$) du champ magnétique terrestre. Cette équation est l’analogue de l’ellipsoïde de gravité théorique, mais qui décrit le potentiel du champ géomagnétique. Il est important de noter que la loi de Gauss ne permet pas une valeur de $n=0$ dans la somme, car le résultat correspondrait au potentiel d’un monopôle magnétique.
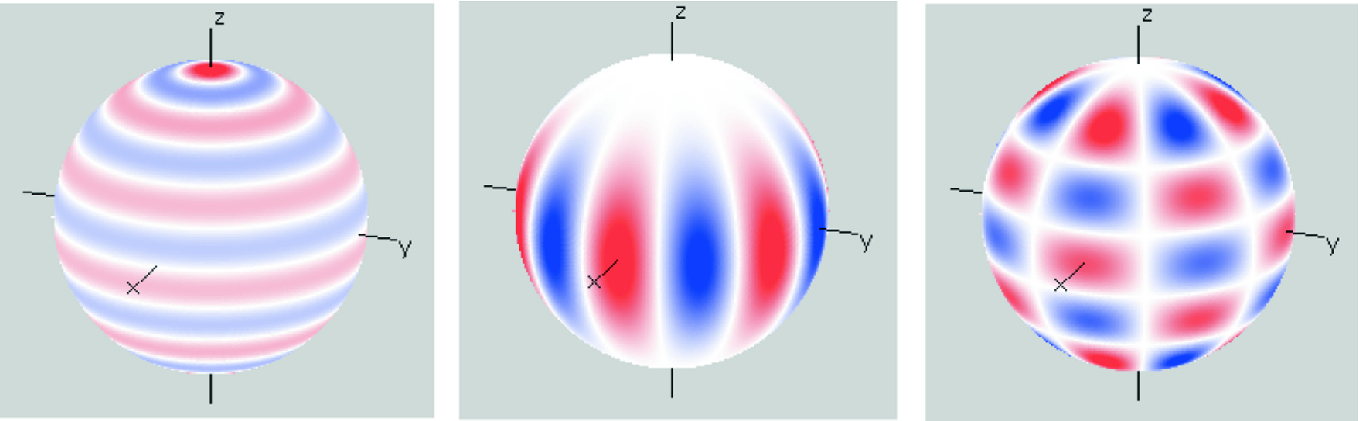
Figure 3. Visualisation des harmoniques sphériques. À gauche : n = 11, m = 0. Au centre : n = 6, m = 6. À droite : n = 8, m = 4. Source.
Finalement, à l’échelle du système solaire, le champ magnétique de la Terre s’apparente à celui d’un dipôle.
Sources du champ magnétique
D’après les équations de Maxwell, le champ géomagnétique doit théoriquement être causé par une source interne ou externe. Ces sources peuvent être rémanentes (aimants permanents) ou être générées par un flux de densité de courant quelconque. L’analyse du champ géomagnétique observé à la surface du globe démontre qu’environ 99 % provient de sources internes, par rapport à 1 % qui proviendrait de sources externes à la Terre. Le champ géomagnétique qui est généré par des processus à l’intérieur de la Terre s’apparente à celui d’un dipôle. Par contre, la Terre est continuellement exposée aux émissions de plasma (un gaz de particules chargées électriquement) du Soleil. L’interaction de ses particules avec le champ magnétique de la Terre dans la magnétosphère et les courants générés dans l’ionosphère par la rotation de la Terre sont les sources externes du champ géomagnétique.
Toujours selon l’analyse des harmoniques sphériques, les contributions des sources internes sont :
\[T_n^i = \sum_{m=0}^n (g_n^{mi}\cos{m\phi} + h_n^{mi}\sin{m\phi})\ P_n^m(\theta) ,\]où $\phi$ est la longitude et $\theta$ est la colatitude (en coordonnées sphériques). $P_n$ est le polynome associé de Legendre de degré $n$ et d’ordre $m$. Les termes $g_n$ et $h_n$ sont appelés coefficients de Gauss et ont les mêmes unités que le champ magnétique (tesla). De la même façon les contributions des sources externes sont :
\[T_n^e = \sum_{m=0}^n (g_n^{me}\cos{m\phi} + h_n^{me}\sin{m\phi})\ P_n^m(\theta) .\]Ces termes sont insérés dans l’équation (9) pour obtenir le potentiel partout sur la surface du globe. Dans la pratique on réunit les contributions externes et internes en un seul terme pour obtenir le modèle de l’International Geomagnetic Reference Field (IGRF). Le modèle est mis à jour à chaque 5 ans par l’Association internationale de géomagnétisme et d’aéronomie (AIGA) avec de nouveaux coefficients de Gauss pour s’adapter aux variations naturelles du champ magnétique. La liste des coefficients pour les 13 premiers degrés de l’expansion en harmoniques sphériques sont donnés par l’IGRF.
Modélisation du champ magnétique
Le modèle de l’IGRF donne le potentiel scalaire magnétique partout sur la Terre. Pour obtenir le champ magnétique, on utilise le fait qu’il est conservatif ($\boldsymbol{B} = -\nabla V$) et on obtient :
La composante vers le Nord :
\[\begin{align} B_x & = -B_{\theta}\\ & = \frac{1}{r}\frac{\partial V}{\partial\theta} \end{align}\]La composante vers l’Est :
\[\begin{align} B_y & = -B_{\phi}\\ & = -\frac{1}{r\sin{\theta}}\frac{\partial V}{\partial\phi} \end{align}\]Et la composante vers le bas :
\[\begin{align} B_z & = -B_{r}\\ & = \frac{\partial V}{\partial r} \end{align}\]Cartes isomagnétiques 2020–2025
Les cartes isomagnétiques sont des cartes de contour qui montrent les différentes composantes du champ magnétique, comme sa déclinaison et son inclinaison (en degrés) son amplitude totale et ses composantes verticale et horizontale (en nT). Les cartes présentées dans cette section ont été produites par le British Geological Survey (BGS), qui contribue à l’élaboration de l’IGRF. Vous pouvez peut retrouver les cartes originales en pleine résolution sur le site web du BGS.
Déclinaison
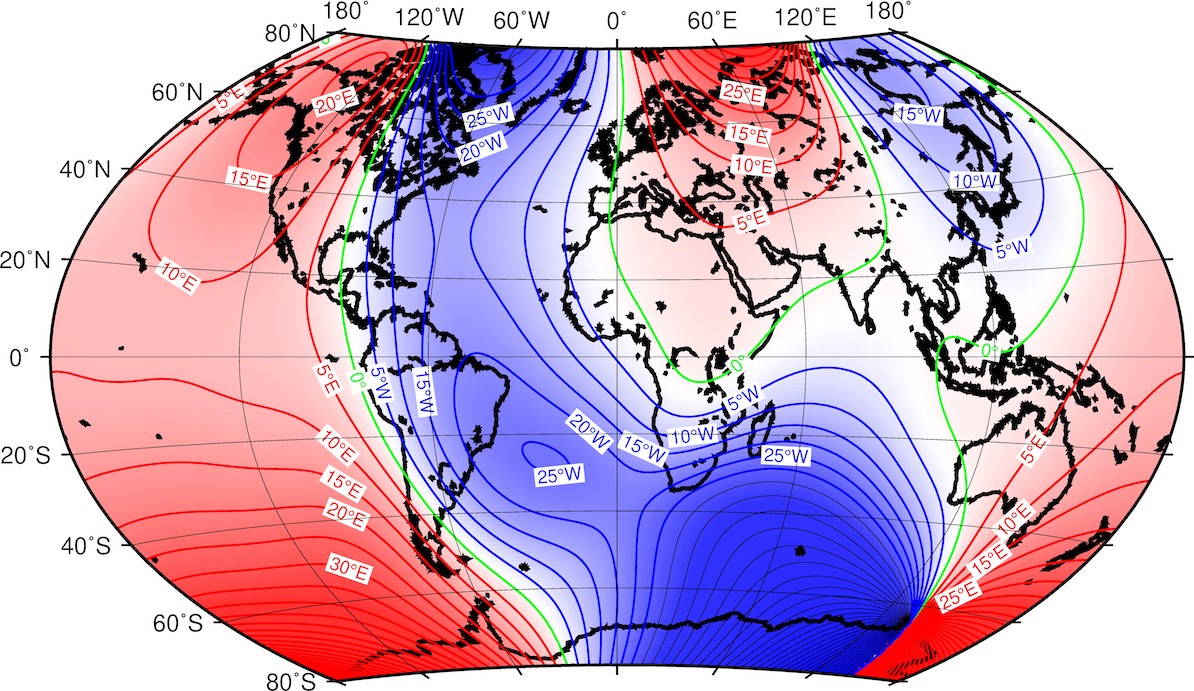
Figure 4. Carte isomagnétique de la déclinaison du champ géomagnétique.
Inclinaison
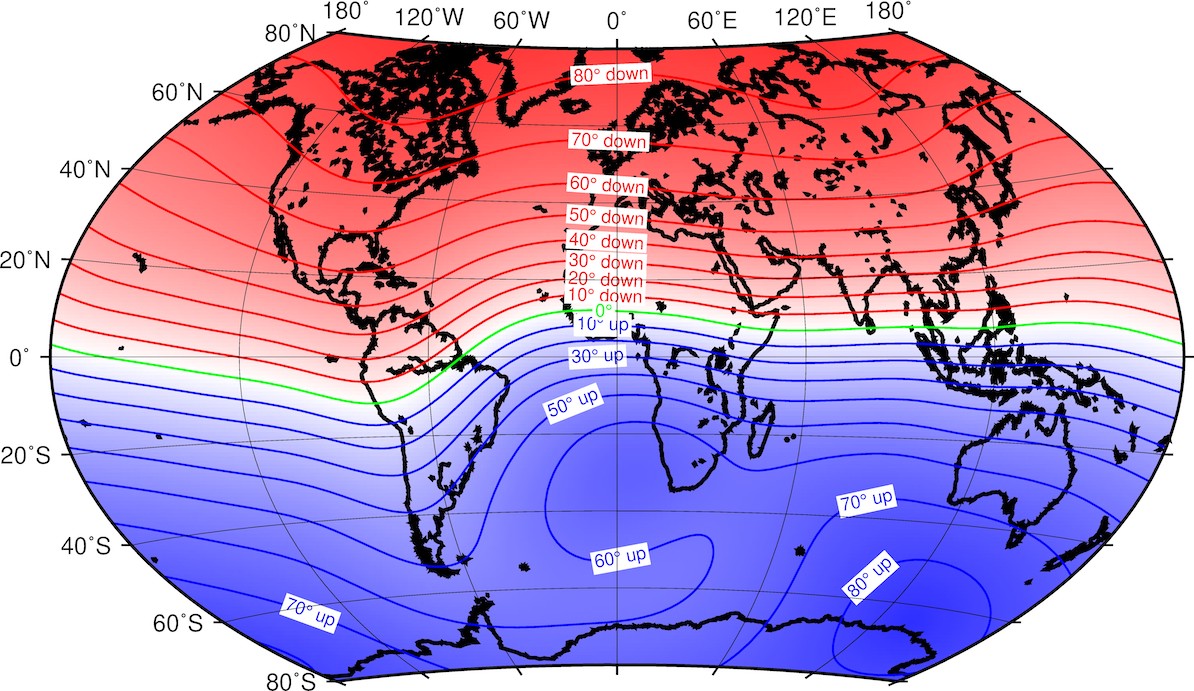
Figure 5. Carte isomagnétique de l’inclinaison du champ géomagnétique.
Champ total
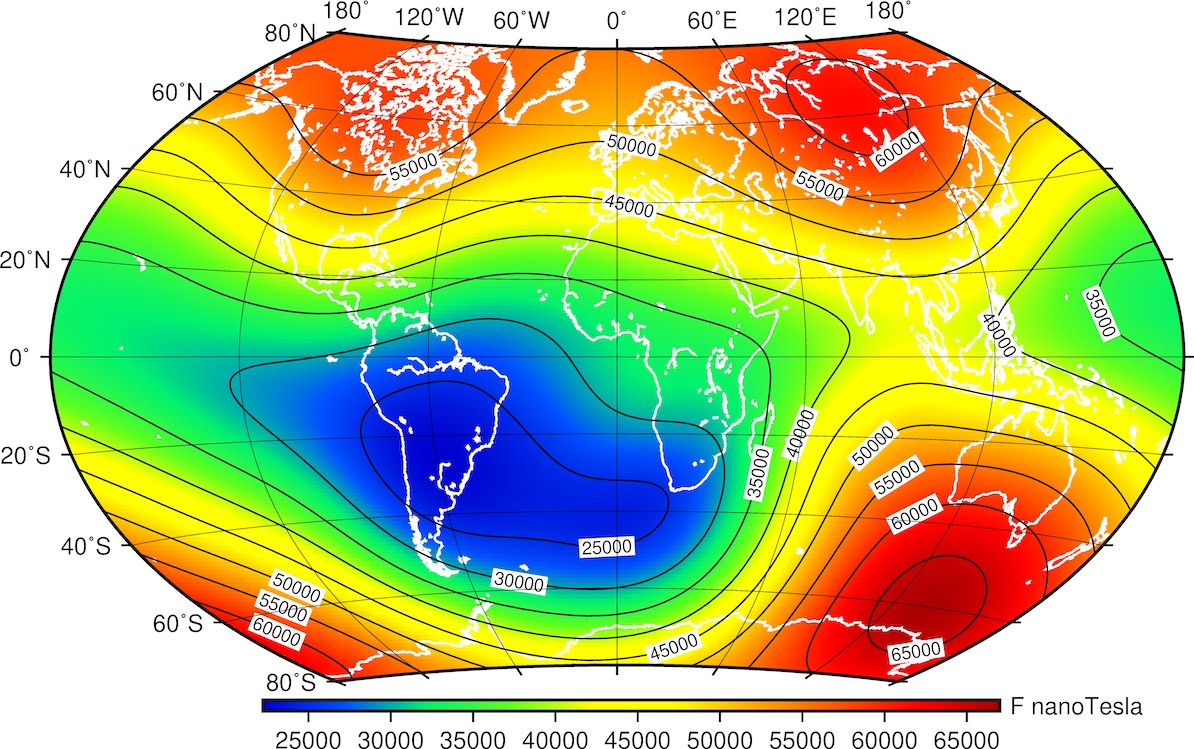
Figure 6. Carte isomagnétique de l’amplitude du champ géomagnétique.
Composante verticale
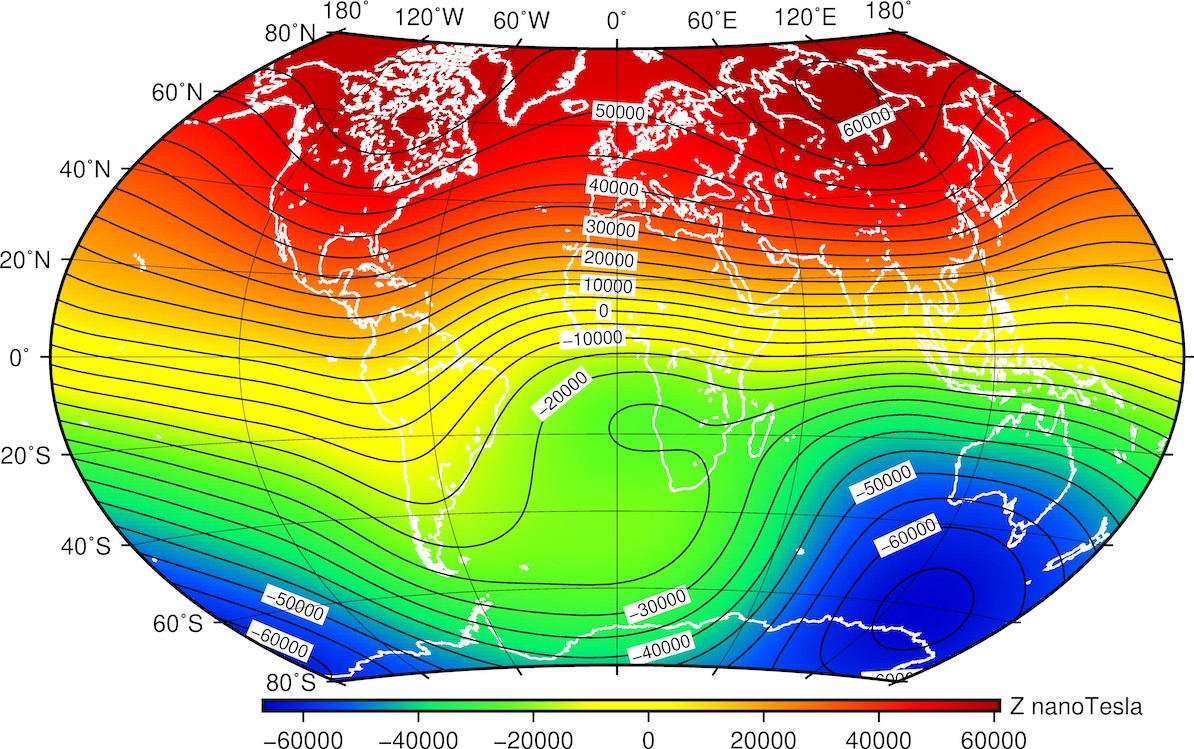
Figure 7. Carte isomagnétique de la composante verticale du champ géomagnétique.
Composante horizontale
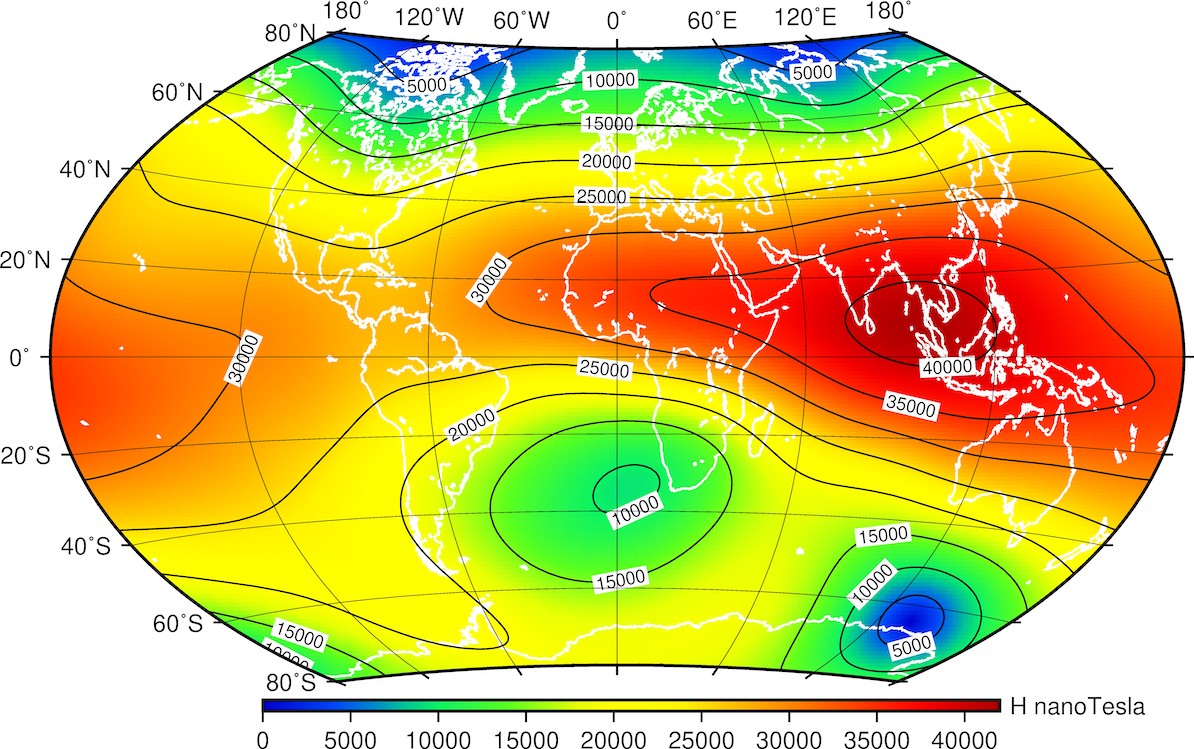
Figure 8. Carte isomagnétique de la composante horizontale du champ géomagnétique.
Autres ressources
Consultez cette page de NOAA pour voir plus de cartes isomagnétiques de l’IGRF produites pour la période 2020–2025.