4.3.3 Dipôle magnétique
Formulation générale
Dans la section 4.2.5, on a vu que les anomalies du champ total ($\Delta T$) recherchées avec la méthode magnétique correspondent à
\[\Delta T \approx \boldsymbol{\hat{F}} \cdot \boldsymbol{\Delta F} ,\]où $\boldsymbol{\Delta F}$ est une perturbation dans le champ régional (le champ primaire) causée par la géologie. Si cette perturbation est causée par un corps d’aimantation $\boldsymbol{M}$ et de volume $v$ dont le potentiel est (section 4.3.2)
\[V(P) = -C_m \int_v \boldsymbol{M} \cdot \nabla \frac{1}{r}\ dv ,\]on en déduit que la perturbation est
\[\boldsymbol{\Delta F} = -C_m \nabla \int_v \boldsymbol{M} \cdot \nabla \frac{1}{r}\ dv\]et donc que
\[\Delta T = -C_m \boldsymbol{\hat{F}}\cdot\nabla \int_v \boldsymbol{M} \cdot \nabla \frac{1}{r}\ dv .\]Solution numérique
L’équation (4) doit être résolue numériquement, sauf pour les géométries simples où on peut la résoudre analytiquement. En pratique, on va utiliser une stratégie semblable à celles déjà décrites dans la section 2.4.
Par exemple, pour une géométrie quelconque qui possède une aimantation non-uniforme (Figure 1), on divise le volume en plusieurs petites composantes comme des prismes ou des dipôles. Si la discrétisation est assez fine, on peut faire l’approximation que l’aimantation est uniforme dans chaque cellule.
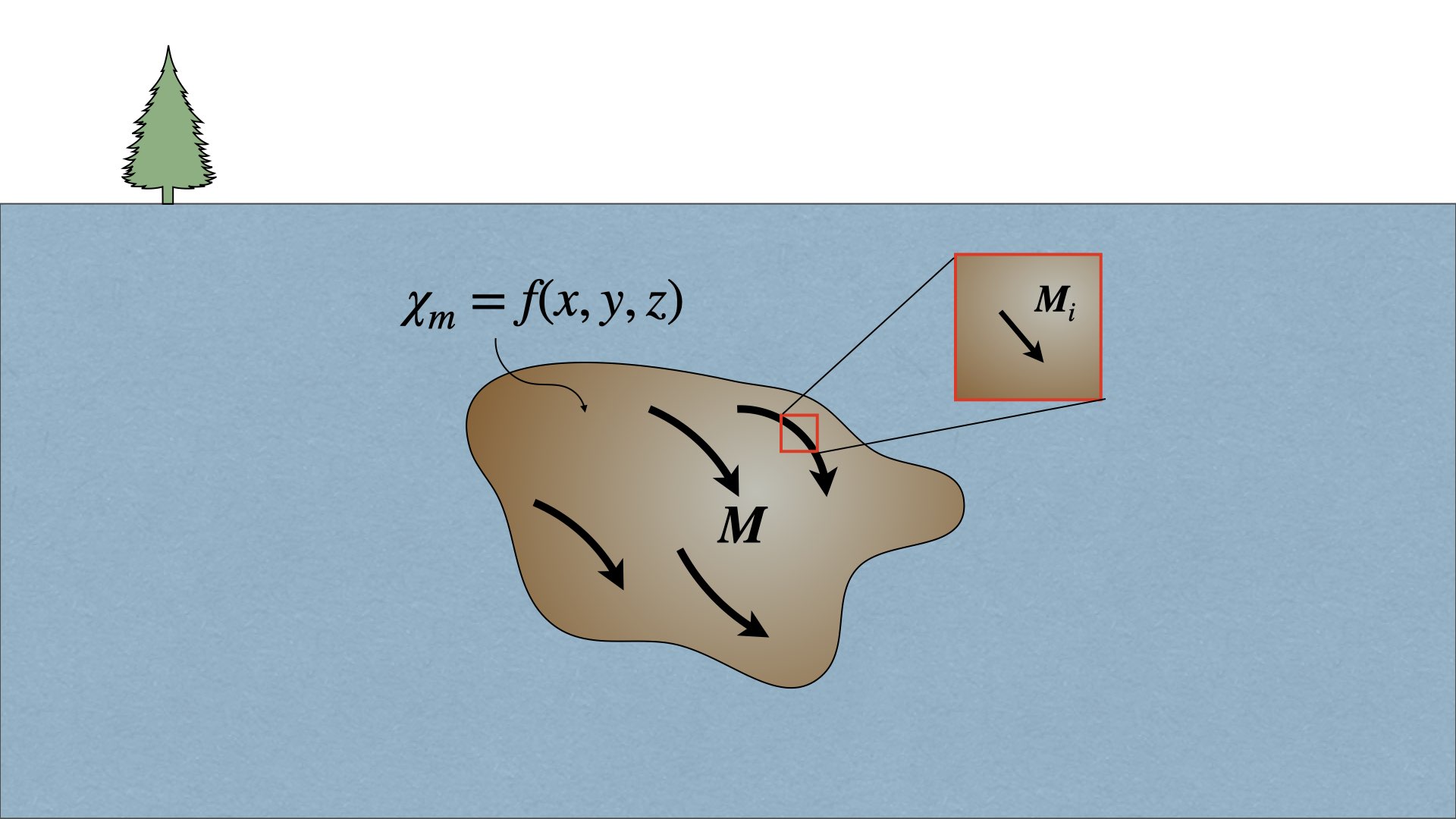
Figure 1. Schéma montrant une aimantantion uniforme dans une petite cellule d’un volume discrétisé. L’aimantation dans le volume total n’est pas uniforme, car la susceptibilité magnétique du matériau n’est pas homogène.
Pour un modèle discretisé en $N$ cellules et dont le volume de chaque cellule est $V_i$, la perturbation du champ primaire (l’équation 3) devient
\[\boldsymbol{\Delta F} = \sum_{i=1}^N M_i \boldsymbol{b}_i,\]avec
\[\boldsymbol{b}_i = -C_m V_i \nabla \left( \boldsymbol{\hat{M}}_i \nabla \frac{1}{r} \right).\]Modélisation d’un dipôle en 3D
Dans cette section on va montrer comment prédire l’anomalie de champ total d’un corps aimantable qui baigne dans un champ magnétique d’intensité $F$ (en tesla), d’inclinaison $I$ et de déclinaison $D$. Pour un corps simple caractérisé par une susceptibilité magnétique $\chi_m$ et un volume total $v$, celui-ci peut être paramétrisé comme un dipôle de moment
\[m = \chi_m H v ,\]où $H = F/\mu_0$.
Équation du dipôle
On part de l’équation de l’anomalie de champ total
\[\Delta T \approx \boldsymbol{\hat{F}} \cdot \boldsymbol{\Delta F} ,\]et on sait que pour un dipôle :
\[\boldsymbol{\Delta F} = C_m \boldsymbol{m}\cdot\nabla\nabla\left(\frac{1}{r}\right) ,\]où $r = \sqrt{x^2 + y^2 + z^2}$.
Le terme $\nabla\nabla\left(\frac{1}{r}\right)$ correspond à la matrice hessienne ($\mathbf{J}$) suivante :
\[\begin{align} \mathbf{J} &= \begin{pmatrix} \frac{\partial^2}{\partial x^2} & \frac{\partial^2}{\partial x\partial y} & \frac{\partial^2}{\partial x\partial z} \\ \frac{\partial^2}{\partial y\partial x} & \frac{\partial^2}{\partial y^2} & \frac{\partial^2}{\partial y\partial z}\\ \frac{\partial^2}{\partial z\partial x} & \frac{\partial^2}{\partial z\partial y} & \frac{\partial^2}{\partial z^2} \end{pmatrix} \left(\frac{1}{r}\right), \\ \mathbf{J} &= \begin{pmatrix} \frac{3x^2}{r^5} - \frac{1}{r^3} & \frac{3xy}{r^5} & \frac{3xz}{r^5}\\ \frac{3xy}{r^5} & \frac{3y^2}{r^5} - \frac{1}{r^3} & \frac{3yz}{r^5}\\ \frac{3xz}{r^5} & \frac{3yz}{r^5} & \frac{3z^2}{r^5} - \frac{1}{r^3} \end{pmatrix}. \end{align}\]Qu’est-ce qu’une matrice hessienne? Faites l’exercice pour vous convaincre, le premier opérateur $\nabla$ transforme la fonction scalaire $1/r$ en vecteur cartésien (définition du gradient d’un scalaire). Puis, le deuxième opérateur $\nabla$ transforme ce vecteur en matrice (définition du gradient d’un vecteur). Le résultat est une matrice hessienne, c’est-à-dire une matrice décrivant toutes les dérivées de second ordre de la fonction $1/r$.
Le vecteur unitaire $\boldsymbol{\hat{m}}$ est un vecteur de rotation qui tient compte de l’inclinaison et de la déclinaison du champ, ces composantes sont des cosinus directeurs :
\[\boldsymbol{m} = \begin{pmatrix} m_x\\ m_y\\ m_z \end{pmatrix} = m\begin{pmatrix} \cos(I)\cos(D)\\ \cos(I)\sin(D)\\ \sin(I) \end{pmatrix} .\]On obtient finalement que la perturbation dans le champ primaire est
\[\boldsymbol{\Delta F} = C_m \boldsymbol{m}\cdot\mathbf{J}\]et donc l’anomalie de champ total est
\[\Delta T = C_m \boldsymbol{\hat{F}}\cdot(\boldsymbol{m}\cdot\mathbf{J}) .\]Exemples
Pour calculer l’anomalie de champ total, on va d’abord définir la matrice $\mathbf{J}$ dans une fonction Python puisqu’il faudrait mettre à jour cette matrice pour chaque point du levé.
def calculer_J(x, y, z):
# Retourne la matrice J
r = np.sqrt(x*x + y*y + z*z)
J = np.zeros((3, 3))
J[0, 0] = 3*x**2 / r**5 - 1/r**3
J[1, 1] = 3*y**2 / r**5 - 1/r**3
J[2, 2] = 3*z**2 / r**5 - 1/r**3
J[0, 1] = 3*x*y / r**5
J[0, 2] = 3*x*z / r**5
J[1, 0] = 3*x*y / r**5
J[1, 2] = 3*y*z / r**5
J[2, 0] = 3*x*z / r**5
J[2, 1] = 3*y*z / r**5
return J
Il faudra également calculer $\boldsymbol{m}$ pour une inclinaison et une déclinaison donnée du champ magnétique. C’est une bonne idée de faire ce calcul dans une fonction :
def calculer_direction_m(I, D):
# Retourne un vecteur horizontal des
# cosinus directeurs de l'aimantation
I, D = np.radians(I), np.radians(D)
return np.array([np.cos(I)*np.cos(D),
np.cos(I)*np.sin(D),
np.sin(I)])
Pour calculer l’anomalie de champ total, on commence par déclarer les paramètres du problème.
# Définir les coordonnées
xs = np.linspace(-20, 20, 200) # m
y = 0 # m
z = 5 # m (z est positif vers le bas)
# Définir les paramètres du champ
C_m = 1e-7 # constante
mu_0 = np.pi*4e-7
I = 90 # deg
D = 0 # deg
F = 55000e-9 # tesla
# Définir les paramètres du corps
chi = 1e-3 # susceptibilité magn
v = 1 # volume
m = chi*F*v/mu_0 # moment dipolaire
Et finalement on appelle les fonctions définie plus haut pour calculer l’anomalie à chacune des positions sur l’axe des $x$. Remarquez que $y$ et $z$ pourraient aussi varier et qu’il faudrait boucler sur ces variables pour avoir la réponse à chaque coordonnées $(x, y, z)$. Idéalement, on ferait le calcul de façon vectorielle avec numpy sans boucle, mais une boucle démontre mieux le raisonnement à suivre.
m_chapeau = calculer_direction_m(I, D) # \hat{m}
ts = np.empty(len(xs)) # pour accueillir les résultats
for i, x in enumerate(xs):
J = calculer_J(x, y, z) # la matrice hessienne du champ dipolaire
dF = C_m * np.dot(m * m_chapeau, J) # m*J
dT = np.dot(dF, m_chapeau) # projection sur F
Dans les exemples qui suivent, on étudiera la sensibilité de l’anomalie de champ total créée par un dipôle magnétique enfoui par rapport à différents paramètres comme l’intensité, la déclinaison et l’inclinaison du champ primaire.
Sensibilité à l’intensité du champ
La Figure 2 montre l’effet de l’intensité du champ primaire sur l’amplitude de l’anomalie de champ total générée par un dipôle enfoui.
Figure 2. Profils d’anomalies de champ total créée par un dipôle magnétique pour différentes intensités du champ primaire. Le dipôle est assimilé à un prisme rectangulaire de volume égal à 1 m$^3$, de susceptibilité magnétique égale à 1 SI et situé à une profondeur de 5 m sous la surface. L’inclinaison du champ primaire est $90^{\circ}$ et sa déclinaison $0^{\circ}$.
Remarquez que l’amplitude de l’anomalie est directement proportionnelle à l’amplitude du champ primaire.
Sensibilité à la profondeur du dipôle
La Figure 3 montre l’effet de la profondeur de la source sur l’anomalie de champ total générée par une dipôle enfoui.
Figure 3. Profils d’anomalies de champ total créée par un dipôle magnétique enfoui à différentes profondeurs. Le dipôle est assimilé à un prisme rectangulaire de volume égal à 1 m$^3$, de susceptibilité magnétique égale à 1 SI. L’inclinaison du champ primaire est $90^{\circ}$, sa déclinaison est $0^{\circ}$ et son intensité est 55 000 nT.
Remarquez comment l’anomalie devient rapidement très atténuée dès que la profondeur augmente. C’est parce que l’anomalie de champ total a une dépendance en $1/z^3$ (voir les termes géométriques dans la matrice $\mathbf{J}$).
Sensibilité à l’inclinaison du champ
La Figure 4 montre l’anomalie de champ total d’un prisme de 1 m$^3$ et de suscpetibilité magnétique égale à 1 enfoui à 5 m sous la surface du sol pour différentes inclinaisons du champ magnétique primaire. L’intensité du champ primaire est de 55 000 nT. La déclinaison du champ est $0^{\circ}$ : l’axe des $x$ pointe vers le nord magnétique.
Figure 4. Profils d’anomalies de champ total créées par un dipôle magnétique enfoui avec une inclinaison du champ primaire variable. Le dipôle est assimilé à un prisme rectangulaire situé à 5 m sous la surface, de volume égal à 1 m$^3$ et de susceptibilité magnétique égale à 1 SI. La déclinaison du champ primaire est $0^{\circ}$ et son intensité est 55 000 nT.
Remarquez comment l’anomalie devient asymétrique lorsque l’inclinaison du champ est asymétrique. L’anomalie est positive du côté où les lignes du champ secondaire ($\boldsymbol{\Delta F}$) sont parallèles aux lignes du champ primaire et négative quand elles sont antiparallèles.
La Figure 5 montre les cartes d’anomalie de champ total générées par le même prisme pour différentes valeurs de l’inclinaison du champ.
Figure 5. Cartes des anomalies de champ total créées par un dipôle magnétique enfoui. Le dipôle est assimilé à un prisme rectangulaire situé à 5 m sous la surface, de volume égal à 1 m$^3$ et de susceptibilité magnétique égale à 1 SI. La déclinaison du champ primaire est $0^{\circ}$ et son intensité est 55 000 nT. L’axe des $x$ pointe vers le nord magnétique et l’axe des $y$ vers l’est.
Sensibilité à la déclinaison du champ
La Figure 6 montre les cartes d’anomalie de champ total générées par le même prisme pour différentes valeurs de la déclinaison du champ. L’inclinaison du champ est fixée à $45^{\circ}$.
Figure 6. Cartes des anomalies de champ total créées par un dipôle magnétique enfoui pour différentes déclinaison du champ primaire. Le dipôle est assimilé à un prisme rectangulaire situé à 5 m sous la surface, de volume égal à 1 m$^3$ et de susceptibilité magnétique égale à 1 SI. L’inclinaison du champ primaire est $45^{\circ}$ et son intensité est 55 000 nT. L’axe des $x$ pointe vers le nord magnétique et l’axe des $y$ vers l’est.
Remarquez comment on peut déduire la déclinaison du champ primaire en mesurant l’orientation de l’anomalie.