TP3 - Analyse spectrale
À rendre le 2025-04-06 - 7% du cours
Contexte
Le TP3 porte sur la caractérisation des sites de stockage de carbone avec la méthode de gravimétrie, tel que démontré en classe avec l’étude de cas de Andrés et al. (2016). Un levé gravimétrique a été réalisé à Hontomín, Espagne avec pour objectif de calculer l’étendue d’un piège géologique pour stocker le CO$_2$.
Objectifs
Objectifs généraux
- Apprendre à filtrer des données géophysiques dans le domaine spectral.
- Comprendre l’utilité et les limites des différents filtres géophysiques.
Objectifs spécifiques
- Corriger les données gravimétriques fournies et obtenir l’anomalie de Bouguer.
- Calculer l’anomalie régionale et l’anomalie résiduelle en effectuant un prolongement vers le haut de 100 m sur l’anomalie de Bouguer.
- Calculer les dérivées spatiales de l’anomalie de Bouguer.
- Estimer le volume du piège géologique sur le site prévu pour le stockage de CO$_2$ et valider cette estimation par modélisation 3D.
Données
Veuillez télécharger les données du levé gravimétrique ici : TP3-GRAVITE-CO2.csv. Toutes les données sont fournies dans les unités SI.
- Le levé contient 10 201 stations espacées de 20 m sur une grille uniforme carrée.
- La station de base est située aux coordonnées $(x, y) =(-1000, -1000)$.
- La correction de dérive a déjà été effectuée sur les données, mais celles pour l’altitude, le plateau et la latitude n’ont pas été effectuées.
- Trois forages verticaux interceptent le toît du piège à 50 m de profondeur.
- Le forage F1 à la position $(-200, 0)$ confirme une épaisseur du piège de 75 m.
- Le forage F2 à la position $(100, -200)$ confirme une épaisseur du piège de 100 m.
- Le forage F3 à la position $(50, 150)$ confirme une épaisseur du piège de 125 m.
La topographie et l’emplacement des forages sur le site sont montrés à la Figure 1.
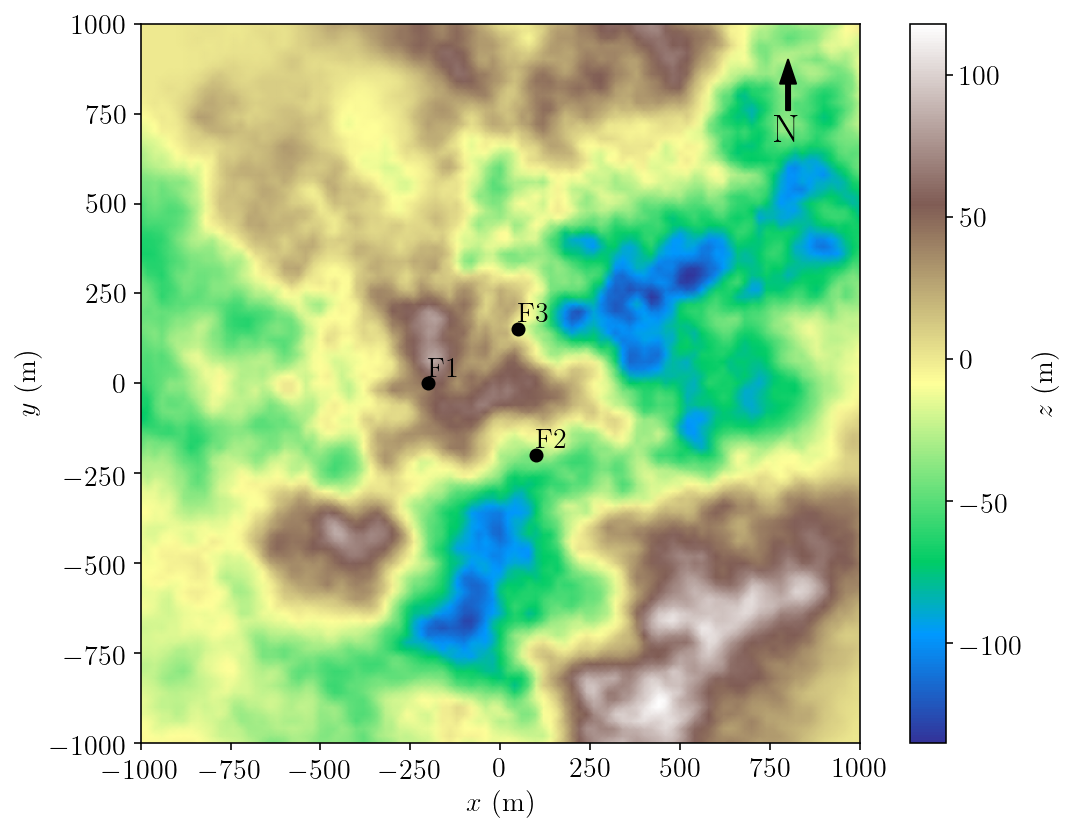
Figure 1. Carte topographique du site à l’étude.
Exemples pour démarrer
Librairies
import numpy as np # calculs numériques
import pandas as pd # gestion des données
import matplotlib.pyplot as plt # graphiques
Carte de couleur
La Figure 2 est une carte de la gravité observée sur le site du levé géophysique. Cette carte est produite avec la librairie Matplotlib et plus précisément avec la fonction plt.imshow(). Il est recommandé d’utiliser ce gabarit pour vos cartes remises dans le compte-rendu.
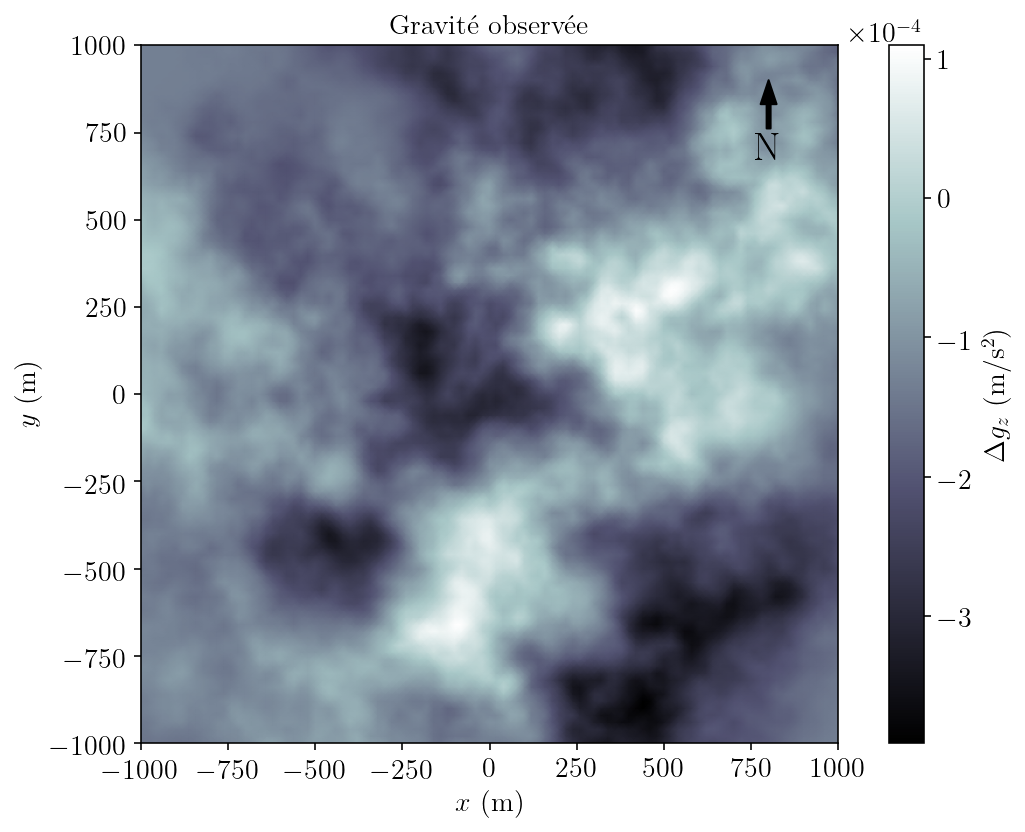
Figure 2. Carte de la gravité observée sur le site à l’étude.
Pour créer une carte à partir d’un vecteur de coordonnées $X, Y, Z$ avec plt.imshow(), il faut modifier la forme des vecteurs avec reshape() pour qu’ils soient des matrices carrées :
extent = [df['X'].min(),
df['X'].max(),
df['Y'].min(),
df['Y'].max()]
plt.imshow(
df["Z"].values.reshape(ny, nx),
interpolation='gaussian',
origin='lower',
aspect='equal',
extent=extent,
cmap="bone",
)
# Où ny et nx sont le nombre de pixels voulu en y et en x, respectivement.
Fonction pour calculer l’anomalie régionale
La fonction suivante prend des vecteurs de coordonnées x et y ainsi qu’un vecteur de l’anomalie de Bouguer gz et retourne la gravité prolongée à une hauteur h.
def calcul_regionale(x, y, gz, h):
"""Calcule le prolongement du champ `gz` à une hauteur `h`.
Args:
x (1d array): Vecteur des coordonnées x.
y (1d array): Vecteur des coordonnées y.
gz (1d array): Vecteur de l'anomalie de Bouguer.
h (float): Hauteur du prolongement en mètres.
Returns:
array: L'anomalie régionale.
"""
# Préparation des données et padding
dim = (len(y.unique()), len(x.unique()))
gz = gz.values.reshape(dim)
gz = np.pad(gz, dim, 'reflect') # pad autour de la carte
# Transformation de Fourier
gz_hat = np.fft.fft2(gz)
k_x = 2 * np.pi * np.fft.fftfreq(n=3*dim[1], d=x.diff().max()) # calcul kx
k_y = 2 * np.pi * np.fft.fftfreq(n=3*dim[0], d=y.diff().max()) # calcul ky
KXX, KYY = np.meshgrid(k_x, k_y) # mettre kx et ky en grille
# Opération de filtrage dans le domaine spectral
gz_hat *= np.exp(-h * np.sqrt(KXX**2 + KYY**2))
# Transformation inverse
regionale = np.fft.ifft2(gz_hat).real
regionale = regionale[dim[0]:-dim[0], dim[1]:-dim[1]] # enlève le padding
return regionale.flatten() # vecteur des données filtrées
Exemple d’utilisation :
df['Regionale'] = calcul_regionale(df['X'], df['Y'], df['Bouguer'], h=100)
Gravité d’un prisme rectangulaire
La composante verticale la gravité mesurée aux coordonnées d’observations $x, y, z$ et causée par un prisme rectangulaire de constrate de densité $\Delta\rho$ dont les côtés sont aux coordonnées $x_i, y_j, z_k$ est (Li & Chouteau, 1998)
\(\Delta g_z = G \Delta\rho \sum_{i=1}^2 \sum_{j=1}^2 \sum_{k=1}^2 \mu_{ijk} \left[ \Delta x_i \ln{}(\Delta y_j + r_{ijk}) + \Delta y_j \ln{}(\Delta x_i + r_{ijk}) - \Delta z_k \arctan{\frac{\Delta x_i \Delta y_j}{\Delta z_k r_{ijk}}} \right]\),
où $G$ est la constante gravitationnelle,
$ \Delta x_i = x - x_i $,
$ \Delta y_j = y - y_j $,
$ \Delta z_k = z - z_k $,
$ r_{ijk} = \sqrt{\Delta x_i^2 + \Delta y_j^2 + \Delta z_k^2} $
et
$ \mu_{ijk} = (-1)^i (-1)^j (-1)^k $,
avec l’axe des $z$ défini vers le haut. Si l’axe des $z$ est défini vers le bas, il faut ajouter un facteur $-1$ devant l’équation.
Indices
- Les dérivées spatiales sont $\partial/\partial x$, $\partial/\partial y$, $\partial/\partial z$, $\partial^2/\partial z^2$, le gradient horizontal et le signal analytique.
- Il est recommandé de créer une fonction Python pour chaque filtre.
- Il est recommandé d’enregistrer les résultats des filtres sous de nouvelles colonnes.
Références
- Andrés, J., Alcalde, J., Ayarza, P., Saura, E., Marzán, I., Martí, D., Martínez Catalán, J. R., Carbonell, R., Pérez-Estaún, A., García-Lobón, J. L., & Rubio, F. M. (2016). Basement structure of the Hontomín CO2 storage site (Spain) determined by integration of microgravity and 3-D seismic data. Solid Earth, 7(3), 827‑841. https://doi.org/10.5194/se-7-827-2016
- Li, X., & Chouteau, M. (1998). Three-Dimensional Gravity Modeling In All Space. Surveys in Geophysics, 19(4), 339‑368. https://doi.org/10.1023/A:1006554408567